Robot Manipulator and Underwater Robot Application 5주차 5-4 D-H approach

D-H approach

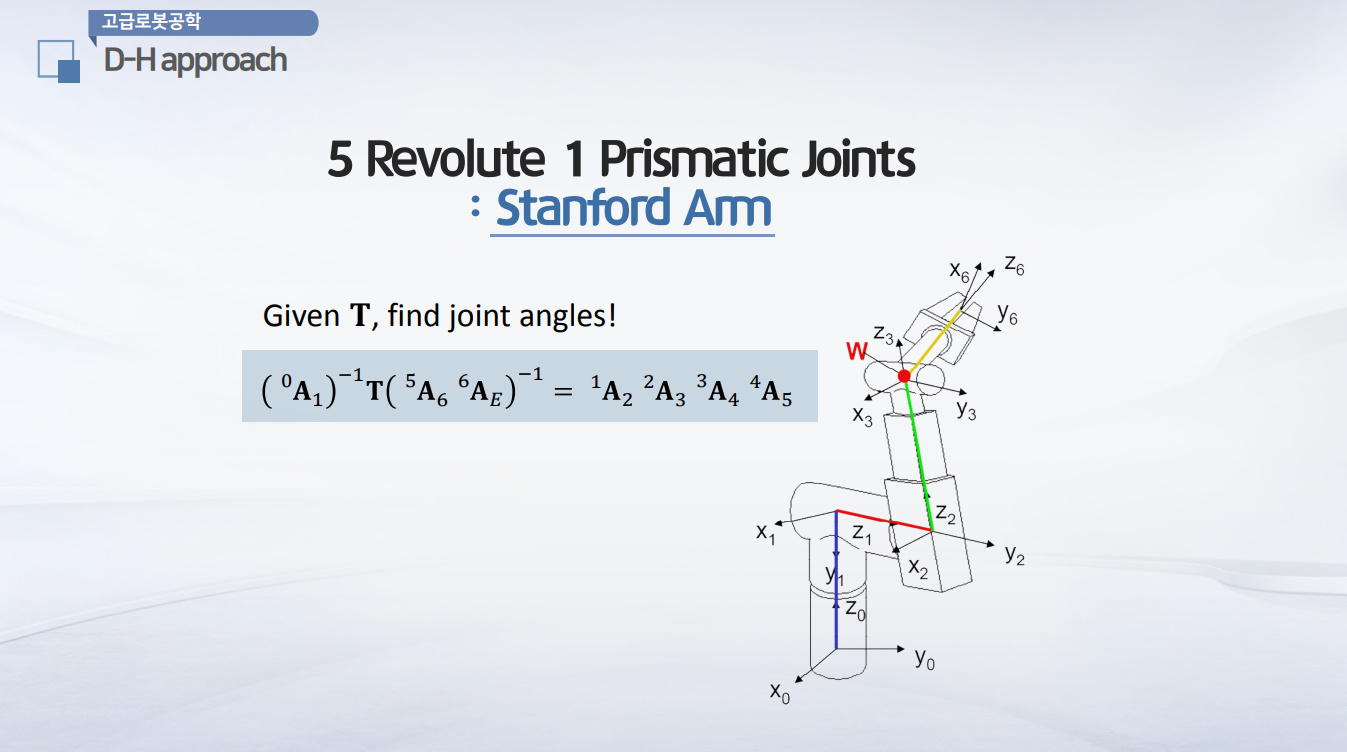
순기구학, Forward Kinematics에서 살펴봤던 stanford arm, 즉 다섯개의 revolute joint와 한 개의 prismatic joint로 이뤄진 Stanford arm에 대해서 Forward Kinematics를 어떻게 구하는지를 살펴봤습니다.
그렇게해서 최종적으로 말단장치에서부터 베이스까지 오는 Transformation Matrix $T$를 구해봤습니다.

이렇게 $T$를 구했을 때 이렇게 주어진 상태에서 만약의 끝점의 위치와 각도를 이렇게 갔으면 좋겠다 라고 주어졌을 때 어떻게 $\theta_1$ 부터 $\theta_6$까지를 구할 수 있을지를 생각할 수 있습니다.

이랬을 때 이 $T$를 활용하는 방법을 가지고 옆에 보이는 식 처럼 원래는 $A_0$에서 1까지, 1에서 2까지, 2에서 3까지 각각 옆으로 쭉 곱해져서 마지막으로 5에서 6까지 곱해진 형태였는데 거기서 한단계 더 나아가서 만약에 end effctor라고 하는 것을 별도의 하나의 프레임으로 분할을 한다면
6부터 end effector 까지 또는 6부터 어떤 특정하게 원하는 좌표까지 이렇게 하나의 변환을 더 추가한다고 가정 했을 때,

총 $A_0$에서부터 1까지부터 시작해서 7개의 매트릭스로 구성이 되는 $T$매트릭스를 앞뒤에다가 inverse transformation을 표현하는 $(^0A_1)^{-1}$를
앞쪽에다가 곱해주게 되면 결과적으로는 우측변에 있는 7개의 매트릭스 중에 하나를 제거 해 줄 수가 있고 마찬가지로 맨 뒷쪽에 $A$의 5에서부터 6, 6에서부터 end effector까지 가는 변환에 대한 inverse를 곱해주게 된다면 마찬가지로 우측변에서 5에서6, 6에서 end effector까지 가는 그러한 변환을 제거해 줄 수가 있게됩니다.

이렇게 제거해주는 이유는 처음 base point부터 끝점까지 가는 변환에 있어서 6개의 좌표계를 전부다 한번에 고려를 해서 6개의 조인트값을 동시에 고려를 해서 구한다는 것은 사실상 쉬운일이 아닙니다.

그래서 이 부분을 조금 간단하게 접근하기 위한 방법을 쓰기 위해서 이렇게 하는 것입니다.

이렇게 일반적인 공간상에서 구동되는, 공간상에서의 manipulator의 경우에는 대부분 사람의 손목에 해당하는 wrist 조인트, 손목조인트가 존재하게 됩니다.
이 조인트는 앞서서 forward kinematics에서 D-H parameter를 구할 때도 역시 그러한 문제를 본적이 있었는데요.
세개의 축이 교차하는 경우가 생깁니다. 세개의 축이 교차한다는 의미는 그 세개의 축의 원점이 같다는 얘기입니다. 이 점을 주로 이용할 것입니다.
그래서 대부분의 3차원상에서 구동되고 있는 여러 다축 manipulator의 경우에는 항상 이 손목을 잘 활용하게 됩니다.
그것을 활용하기 위해서 이와 같이 먼저 주어져있는 전체적인 Transformation Matrix를 이와 같이 간단하게 바꾸기 위한 노력을 했습니다.

이렇게 바꿔졌을 경우에 앞서서 말씀드렸던 것 처럼 $W$, wrist의 포인트 위치는 생각해보시면 base frame에서 1번 프레임, 1번프레임에서 2번 프레임, 2번프레임에서 3번 프레임
즉, $\theta_1$ $\theta_2$ 그리고 2번프레임에서 3번프레임까지 오는 $d_3$ 이렇게 세 개의 값으로만 $W$를 표현할 수 있다는 것을 알 수 있습니다.

이렇게 $T$를 주어진 값을 활용할 건데 이렇게 주어진식을 앞서서 정의했던 것 처럼 $T$값은 정해졌구요, $A$의 1에서부터 2까지 2에서부터 3까지 3에서부터 4까지 4에서부터 5까지 즉 이 리스트에 의한 식,
이 네가지 식이 위에서 살펴본 것 처럼 이렇게 주어졌기 때문에 여기에서 A의 0에서 1까지 5에서부터 6까지를 어떻게 활용을 해서 하나 하나 솔루션을 찾아나갈지를 한번 살펴보도록 하겠습니다.

이 식을 진행하기에 앞서서 전부 구했었던 D-H parameter를 이용해서 바로 Transformation Matrix를 먼저 정의할 필요가 있겠죠.

그래서 이렇게 주어져있는 D-H parameter를 활용을 해서 이와 같이 5에서부터 6까지 오는 변환, 그리고 5에서부터 6까지 오는 변환의 역변환이 필요합니다.
그래서 5에서부터 6까지 오는 변환과 역변환을 옆에있는 이러한 수식처럼 구해낼수가 있습니다. 마찬가지로 0에서부터 1번까지 오는 변환, 0에서부터 1번까지 오는 변환에 대한 역변환도 필요합니다.
이와 같이 이 변환식들을 활용을 하면 앞서서 보여드렸던 수식에 있는 두가지 inverse 파트를 채워넣을 수 있게 되는 것입니다.

그래서 이 두식을 활용을 해서 이와 같이 주어진 $T$에다가 앞뒤에 이 수식을 집어넣어서 계산을 하게 되면, 여기 … 이라고 표시되어 있는 수식에서의 부분들은 로테이션, 즉 각도를 표현하는것을 의미합니다.
우리는 앞서 나왔던 식에서 $W$의 위치만을 활용해서 구해내려고 하는 것이기 때문에 앞에있는 …은 일단은 잊어버리시고, 위치의 의미를 가지고 있는 오른쪽 위쪽에 있는 위치벡터를 뽑아서
이러한 위치벡터를 각각 $P_x$ $P_y$ $P_z$라는 표현을 써서 뽑아보도록 하겠습니다.

이렇게 뽑아놓은 것 중에서 각각 $P_x^{\ast} = –a_xl_2 + P_x$이고 $P_y^{\ast} = –a_yl_2 + P_y$ 그리고 $P_z^{\ast} = –a_zl_2 +P_z$가 되겠습니다.

이렇게 주어진 식을 이용해서 앞서서 $W$를 구했을 때 $W$에서도 마찬가지로 포지션만 사용을 하고 오리엔테이션은 사용하지 않았습니다.
이렇게 두 개로 얻어진 $d_3s_2$는 금방 구했던 수식에 의해서 즉, $a$의 Transformation 0에서부터 1까지, 5에서부터 6까지에 대한 식과 주어진 $T$로 주어진 그 식과 앞서서 $W$를 바로 구했었던
이 식을 활용을 해서 이와 같이 (1) (2) (3)과 같은 세 개의 수식을 만들어 낼 수 있겠습니다.
여기에서 보시면 이 주어진 수식에서는 결과적으로 이 세개의 수식과 세 개의 미지수가 정해지게 되는데,
그 세개의 수식과 세개의 미지수를 바탕으로 즉, $\theta_1$ $\theta_2$ 그리고 $d_3$라고 하는 이 세개의 미지수를 어떻게 결정하는지를 살펴보도록 하겠습니다.

먼저 $t$를 $tan(\theta_1 \above 1pt 2)$ 이라고 이렇게 치환을 한번 해보도록 하겠습니다. 그렇게되면 $cos\theta_1$은 $1-t^2 \above 1pt 1+t^2$ 이라고 쓸 수가 있구요.
그 다음에 $sin\theta_1 = 2t \above 1pt 1+t^2$로써 쓰게되고, 이것을 보통 반각공식이라고 얘기를 합니다. 그래서 이렇게 반각공식으로 정의하게 됩니다.

이렇게 정의한 것들을 바탕으로 앞서서 있었던 세번째 수식에다가 $sin$ $cos$에 대해서 각각 집어넣게 됩니다. 이렇게 집어넣게 되면 여러분들 익숙하신 이차방정식입니다.
이차방정식이 이렇게 주어지게 됩니다. 이렇게 이차방정식이 주어지게 되면 우리는 근의공식을 활용할 수 있게 됩니다. 근의 공식을 활용하면 $t$는 위에 보이는 식처럼 $-P_x^{\ast} \pm \sqrt{P_x^{\ast ^2}+P_y^{\ast ^2}-l_1^2} \above 1pt l_1 + P_y^{\ast}$입니다.
여러분들 이제 이 시점에서 $\pm$가 왜 나오는지 감을 잡으실 수가 있겠습니다. 바로 두개, 복수의 솔루션을 얻게 된다는 그런 의미를 갖게되는 것입니다.
$\pm \sqrt{P_x^{\ast ^2}+P_y^{\ast ^2}-;_1^2}$ 이렇게 얻어지게 됩니다. 이렇게되면 여기서 $P_x^{\ast}$, $P_y^{\ast}$, $l_1$은 전부다 알고있는 값입니다.
주어진 값이죠. 이러한 주어진값을 바탕으로 결과적으로는 $t= tan(\theta_1 \above 1pt 2)$ 을 결정할 수 있게 되는 것 입니다.

이렇게 결정이되면, 이 값을 통해서 $\theta_1$은 $2arctan$ 그리고 앞서서 구한 $tan$값을 활용을 해서 $\pm$값을 포함하는 이러한 $\theta_1$을 계산할 수 있게 되는 것 입니다.
이렇게 $\theta_1$을 구하면서 복수의 솔루션을 찾을 수 있다는 것을 염두에 두셔야 합니다.

그 다음으로 이용할 식은, 바로 두 번째 식과 첫 번째 식을 나누는 식 입니다. 앞서서 사용했던 세번째 식을 제외한 첫번째 식과 두번째 식을 활용해서 $\theta_2$를 한번 구해보면 $\theta_2$는 첫번째 식과 두번째 식에서 보시면 $s_2$, $c_2$만 이렇게 포함이 되고 $d_3$는 아직 모르는 값입니다.
모르는 값이지만 $d_3$는 같은 값이니까 $d_3$를 모르더라도 활용을 할 수 있겠구요. 이 두 식을 나눠주게 되면 결과적으로는 $tan$값을 얻게됩니다.

그래서 첫번째 식을 두번째 식으로 나눠주게 되면 이와 같이 $tan$식을 얻게되고, $tan$식을 활용을 해서 $\theta_2$는 $arctan$라는 역변환을 활용해서 이와 같이 구할 수 있게 됩니다.
여기서도 마찬가지로 $\theta_1$에 따라서 $c_1$과 $s_1$의 값이 결정되는데, $\theta_1$은 앞서서 살펴봤던 것 처럼 두 개의 솔루션을 얻는다는 것을 확인할 수 있었습니다.
이렇게 두개의 솔루션을 활용해서 $\theta_2$도 역시 두 개의 솔루션을 갖는다는 것을 확인 할 수가 있습니다.

이렇게 구한 상태에서 첫번째 수식과 두 번째 수식을 제곱을 해서 더해주게 된다면, $d_3$라는 값을 이 두개의 더해진 수식에 의해서 구할 수 있게 됩니다.
위에 보이는 식처럼 $d_3$는 알고있는 값, $P_x^{\ast}$ $P_y^{\ast}$ $P_z^{\ast}$ $l_0$ 값을 활용합니다.
거기에다가 추가적으로 앞서서 구했던 $sin$값과 $cos$값, $s_1$ $c_1$의 값을 대입함으로써 $d_3$의 값을 결정할 수 있게 되는 것 입니다.
세 개의 수식을 이용해서 $\theta_1$ $\theta_2$ 그리고 $d_3$까지 세 개의 수식을 결정할 수가 있게 됩니다.

그러면 $\theta_1$ $\theta_2$ $d_3$는 앞서서의 방법을 통해서 wrist position을 잘 이용해서 그 포지션의 어떤 관계의 식을 활용을 해서 구했습니다. 그럼 다시 수식을 이와 같이 정리해보겠습니다.
0번째부터 1번째, 1번째부터 2번째, 2번째부터 3번째 까지의 변환은 각각 $\theta_1$ $\theta_2$ $\theta_3$를 구했기 때문에 우리가 알고 있는 값, known값이라고 가정을 할 수가 있겠습니다.
이러한 Known값을 inverse를 취해서 역행렬을 취해서 왼쪽에다가 곱해주게 되면, $T$역시 주어진 값이라고 앞서 말씀드렸던 것 처럼
결국에는 앞쪽은 알고 있는 값들 그리고 뒤쪽에 3번부터 6번까지 가는 이 세 개의 변환은 모르는 값으로 이렇게 배치를 할 수 있게 됩니다.
이렇게 배치를 하고 추가적으로 3번 4번 5번의 값들을 구하는지, $\theta_4$ $\theta_5$ $\theta_6$의 값을 어떻게 구하는지 살펴보도록 하겠습니다.

$T’$이라고 하는 것을 새롭게 정의하도록 하겠습니다. $T’$은 우리가 알고 있었던 0에서부터 6번까지 가는 그 변환에다가 0에서부터 3번까지 가는 변환의 역수, 역변환을 이렇게 새롭게 정의를 하게 되면 일반적으로 $T$는 $n$ $o$ $a$ $p$ 이렇게 네 개의 벡터로서 정의가 되고, 물론 이 $n$ $o$ $a$는 Rotation Matrix를 의미합니다. 그랬을 때 그 앞에다가 우리가 알고있는 0에서부터 3번까지가는 변환의 inverse를 곱해주었기 때문에 그것들에 대한 값이 좀 바뀌었습니다. 그렇지만 우리가 알고 있는 값입니다.
주어진 값에다가 구한값을 넣었기 때문입니다. 그래서 이렇게 새롭게 구한 이 값을 앞의식과 구분하기 위해서 프라임이라는 표현으로 새롭게 정의를 해 보도록 하겠습니다.

그렇지만 그 프라임값은 모두 우리가 알고 있는 값입니다. 만약에 우리가 프라임 앞에 3번에서부터 4번까지 가는 inverse를 곱해준다라고 했을 때,
$T’$이라고 되어 있는 것에 3번, 4번에 Transformation Matrix에 inverse를 곱해주게되면 위에 식처럼 {\ast}는 굳이 식을 전개하는데 꼭 필요한 부분이 아니기 때문에 이 값들이 없다는 얘기는 아니고 이 값들은 있지만 표기는 그냥 {\ast}로써 지금 당장 쓰지는 않을 것이라는 의미로써 이렇게 별표로 표시를 했습니다. 그렇게 곱해주게 되면 옆에 보이는 식처럼 각각의 $n_x’$ $n_y’$ $n_z’$ $o_x’$ $o_y’$ $o_z’$ $a_x’$ $a_y’$ $a_z’$ 이라고 되어있는 값들과 $sin$과 $cos$의 네번째 값, $s_4$ $c_4$ 이러한 값들로써 식이 주어지게 됩니다.

이렇게 주어지는 식의 앞에 곱해주게 되었을 경우에는 우측편에는 네번째에서 다섯번째 다섯번째에서 여섯번째로 가는 변환만 남게 됩니다.

이렇게 남게 됐을 때 네번째와 다섯번째 수식, 다섯번째와 여섯번째 수식을 Transformation matrix로 정의하면
옆에보이는 식에서의 우측변처럼, $c_5c_6 – c_5s_6 s_5$ 이런식으로 식이 주어지게 됩니다. 이렇게 두 개의 변환 매트릭스를 활용해서 각각을 비교해 볼 텐데요. 이 변환매트릭스에서 활용할 수 있는 값들이 무엇이 있는지 한번 살펴보도록 하겠습니다.

즉 $s_4$하고 $sin$ 네번째 조인트의 값인 $sin\theta_4$ 와 $cos\theta_4$를 포함한 식이 0이라는 수식으로 이용하기 쉬운 수식이 주어지게 됩니다.
그렇기 때문에 그 수식을 활용해서 $arctan4$ 값을 구할 수가 있겠죠. 그래서 $a_{y’} \above 1pt a_{x’}$을 하게 되면 $\theta_2$는 $arctan$를 활용해서 구할 수 있게 됩니다.
역시 $arctan$ 같은 경우에는 $\theta_4$와 $\theta_4 + \pi$, 즉 $tan$ 같은 경우에는, $\pi$마다, 즉 180도 마다 반복된다는 것을 알 수 있습니다.
따라서 $\theta_4$에 대해서도 두 개의 솔루션을 얻을 수 있다는 것을 확인할 수 있습니다.

다음으로는 (1,3), (2,3) element를 활용하도록 하겠습니다. (1,3)element, (2,3) element를 활용하게 되면, 결국에는 $arctan$ 값, $\theta_5$의 $tan\theta_5$가 주어지게 됩니다.
$tan\theta_5$가 주어지게 됨으로써 $arctan$를 이용해서 $a_{y’}c_4 + a_{y’}s_4 \above 1pt a_{z’}$로 이렇게 식이 주어지게 됩니다.
이렇게 식이 주어지게 됨으로써 $a_{y’}$,$a_{z’}$은 다 알고 있는 값이고 $\theta_4$는 조금전에 구했기 때문에 역시 알고있는 값이 됩니다.
이 값들을 대입함으로써 $\theta_5$를 얻을 수 있게 되는데요. 역시 $\theta_5$ 형태도 두 개의 솔루션을 얻게 되는데, 이 때의 값들은 $arctan$ 값에서 앞서 구했던 것 처럼 $+\pi$의 형태로 쓸 수도 있고 또는 $-\theta\pi$?로 즉 어떤 $tan$값의 경우에는 +값과 -값이 앞의 $\theta_4$의 값에 따라서 바뀔수 있기 때문에 굳이 $+\pi$를 넣어주지 않고
$\theta_4$에 의해서 $\theta_5$가 각각 두 개의 솔루션을 얻게 되는, 부호가 반대로 되는 그런 효과를 얻게 되기 때문에 굳이 $+\pi$를 해서 진행하지는 않습니다.
그래서 $\theta_5$는 앞서 구했던 $\theta_4$에 따라서 부호가 -가 되기도 하고 +가 되기도 하는 것 입니다. 이제 다섯개의 값을 구했습니다.

마지막으로 여섯번째 값을 구해보도록 하겠습니다. 여섯번째 값은 이번에는 (3,1), (3,2) element를 활용하도록 하겠습니다.
(3,1), (3,2) element를 활용했을 때 $\theta_6$는 결국에는 $tan\theta_6$가 위에 보이는 식 처럼 $n_{x’}s_4 + n_{y’}c_4 \above 1pt o_{x’}s_4 + o_{y’}c_4$로 이렇게 주어지게 됩니다.
역시 마찬가지로 이렇게 주어짐으로써 $\theta_6$값을 결정할 수가 있게 되고 이렇게 $\theta_6$를 구했는데 역시 마찬가지로 $tan$값은 항상 복수의 값이 얻어지게 됩니다.
여기서도 마찬가지로 $\theta_4$와 $\theta_4$의 값에 의해서, $\theta_4$가 $+\pi$만큼의 값이 들어감으로써 앞서서 $\theta_5$를 결정할 때 처럼 마찬가지로 $\theta_5$에 대해서 결정을 할 수도 있습니다.
여기서는 $\theta_6$에 대해서 각각 그 값을 활용하지 않고 분자와 분모에 동일하게 부호의 값도 동일한 형태로 반영이 되기 때문에 두개의 값에 의해서 자동적으로 $tan$ 값을 결정하는 것이 아니라 $\theta_6$에다가 $+\pi$의 형태의 솔루션을 가지고 두 개의 솔루션을 찾을 수 있다라는 식으로 접근을 하겠습니다.

마지막으로 구했던 $\theta_4$ $\theta_5$ $\theta_6$의 경우에는, $\theta_4$가 만약에 $\theta_4$와 $\theta_4 + \pi$두개의 값을 갖게 된다면, $\theta_4$는 $\theta_5$로 연결이 되구요 $\theta_5$는 다시 두 개의 값으로 나눠지게 되구요.
그래서 $\theta_6$와 $\theta_6 + \pi$로 두개의 값이 나눠지게 되고, 마찬가지로 $\theta_4 + \pi$는 $-\theta_5$로 가게되고, 그 값에 의해서 다시 $\theta_6$는 $\theta_6$와 $\theta_6 + \pi$로 총 네 가지 케이스에 대해서 얻어지게 됩니다.
그런데 여기에서 만약에 $\theta_5$가 0으로 주어지게 된다면, 여러분들 앞서서 기억하실 지 모르겠지만 stanford arm 같은 경우에는 마지막 손목 조인트들이 ZYZ의 형태로 구성이 되어 있습니다.
제가 앞서서 Euler angle을 설명드릴 때 마찬가지로 설명 했습니다.
ZYZ의 형태에서 Y가 0, 즉 Y가 움직이지 않는 다섯번째 축이 움직이지 않는 형태가 되면 네번째 축과 여섯번째 축은 같은 각도에 대해서 회전하게 됩니다.
즉, $\theta_4$를 돌리는 것과 $\theta_6$를 돌리는 것이 두 가지의 값들이 결과적으로는 끝점, end effector의 입장에서는 같은값을 반영하게 되는 것입니다.
그래서 $\theta_5$가 0이 되는 경우에는 보통 degenerate한다.

즉 네번째 조인트값과 여섯번째 조인트값이 독립적으로 어떠한 각도를 만들어 낼 수 있는게 아니라
$\theta_5$가 0이 됨으로써 만들어낼 수 있는 각도의 어떠한 전체적인 형상이라던지 이러한 기능들이 떨어지게 된다는 얘기가 됩니다.
그래서 일반적으로 이러한 현상은 공간상에서 구동을 하고 있는 3차원 manipulator, 흔히 기구학 해석하는데 많이 활용되는 퓨마560이라고 하는 manipulator
또 Stanford arm 등등 사람의 손목 조인트를 모방한 그러한 manipulator와 같은 경우에는 항상 발생할 수 있는 문제 입니다.

그래서 이러한 부분들을 접근할 때 $\theta_5$에 부분에 있어서는 항상 0의 값이 되는지 이렇게 degenerate되는지를 주의깊게 살펴볼 필요가 있겠습니다.
이렇게해서 total 세가지 방법으로의 역기구학 해석하는 법을 살펴보았구요. 앞선주차에서 Forward Kinematics 더 앞선 주차에서는 Kinematics를 전체적으로 설명하기 위한 위치표현법, 각도표현법 그리고 이것들을 통한 homogeneous transformation에 대해서 살펴보았습니다.
그러한 방법들을 통해서 Forward Kinematics를 구했고 Forward Kinematics에 반대되는 Inverse Kinematics를 구해봤습니다.
여러분들이 어떤 느낌이실지 모르겠지만, 제가 느끼기에는 Inverse Kinematics는 굉장히 manually, 한마디로 수작업으로 모든 것들을 하나하나 계산을 해서 각각의 케이스마다 정해져 있는 룰이 아닌, 그 케이스에 따라서 내가 어떻게 계산을 해서 어떻게 구할 것이라는 어떤 전략을 세워야하는 조금 어렵고 귀찮은 작업이 될 수 있습니다.
그래서 이런것들은 시간이 많이 소요되고 중간에 실수가 많이 발생할 수 있는 단점을 가지고 있습니다.

늘 이러한 방법을 써야하느냐? 그렇진 않고 또 하나의 새로운 방법을 통해서 이러한 문제점을 극복할 수 있는 방법이 있습니다.
예를 들어서 끝점이 어떻게 움직이느냐에 대한 움직임은 결과적으로는 어떤 그 끝점이 속도를 적분을 해서 그 위치를 정한다고 볼 수 있습니다.
따라서 속도측면에서 이 해석을 진행을 하고 그 속도를 계속해서 적분해나간다면, 이 속도에 따라서 마지막 끝점이 결정되는 것을 굳이 이렇게 어렵고 time consuming 한 이런 작업을 거치지 않더라도
어쩌면 결정 할 수도 있을 것입니다. 따라서 이러한 부분들에 대해서는 이어지는 주차에서 속도기구학이라는 내용을 학습함으로써 이러한 부분을 어떻게 활용할 수 있는지 살펴보도록 하겠습니다.