Geometric approach
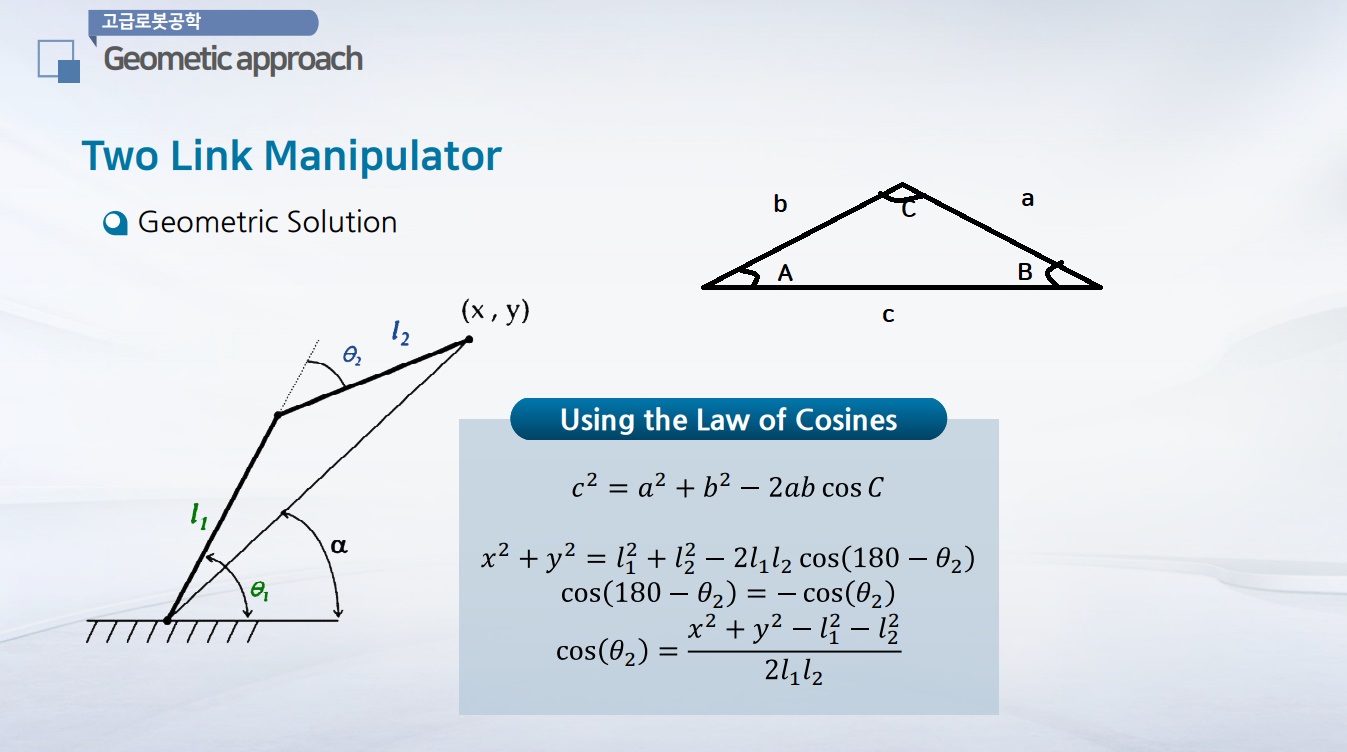
여기에서 주어진 2자유도 Manipulator의 X, Y점이 주어졌을 경우에 각각 구해야 되는 것은 이 $\theta_1$의 각도와 $\theta_2$의 각도입니다
이 Two Link Manipulator의 경우에는 $\theta_2$부터 어떻게 해석할지 먼저 접근을 시작하지만 경우에 따라서는 여러 가지 주어지는 상황에 따라서 여러분들이 어떤걸 먼저 결정해야 되는지 그때그때 바뀌어야 합니다. 그래서 여기에서 주어진 Two Link Manipulator의 방법을 그대로 적용하는 것은 아니고 그때그때마다 주어지는 Manipulator의 상황에 맞게 바뀌어야 된다는 점을 먼저 염두에 두시기 바랍니다.
기하학적인 방법으로 하기 위해서 우리는 먼저 $cos$법칙을 활용해서 $\theta_2$를 결정해볼 텐데요. $cos$ 제2법칙을 이용하면 $c^2 = a^2 + b^2 – 2ab cosC$ 입니다.
$a,b,c$ 라고 하는 세 변의 길이가 주어지고 각각 마주보는 각도를 $ C, B, A$ 라고 했을 때 이 각 변의 길이와 끼인각들의 관계의 식을 설명하는 것이 바로 $cos$ 제2법칙이 되겠는데요.
그래서 $c^2$이 가장 긴 변의 제곱이고 이 값은 $a^2 + b^2$, 즉 나머지 두 변의 제곱을 더하고, 그리고 $-2ab$에 $cos$ 끼인각 $C$의 값을 이용해서 성립하는 법칙입니다.
이것을 2 Link Manipulator에 적용을 하게 된다면 $\sqrt {x^2+y^2}$을 하는 것은 결국 이 길이를 의미하고 이게 C의 역할을 합니다.
그리고 각각 $l_1$ 과 $l_2$의 길이는 주어져있기 때문에 $l_1^2$ $l_2^2$을 집어 넣고 $2l_1l_2$을 끼인각은 결국에는 이 $\theta_2$, $\theta_2$에서 180도에서 $\theta_2$를 뺀 각 만큼 즉, $cos( 180 - \theta_2)$ 만큼의 값을 갖게 됩니다. 여기에서 우리는 $cos$의 성질에 의해서 $cos(180 - \theta_2$는 결국 $-cos(\theta_2)$가 된다는 것을 아실 수 있을 겁니다.
이 성질을 이용해서 결과적으로 $cos(\theta_2)$는 $x^2 + y^2 -l_1^2-l_2^2 \above 1pt 2l_1l_2$이 되겠습니다. 여기에서 좌변의 경우에는 $cos(\theta_2)$ 우변의 경우에는 $l_1 l_2 x y$ 들만의 함수로써 주어져 있습니다.
따라서 모두다 아는 값들이죠. 그래서 이 값을 통해서 $cos(\theta_2)$의 값을 구하고 결과적으로는 $arccos$이라는 것을 이용해서 $\theta_2$를 결정할 수 있게 되는 것입니다.
.jpg)
그러면 이어서, $arccos$을 통해서 $\theta_2$의 값을 얻게 되는데요, 여러분들이 코싸인의 그래프를 생각해보시면, 코싸인 그래프는 이렇게 주어지죠.
그러면 주어지는 어떠한 값들은 그때에 복수의 솔루션을 갖게 되는 것이죠. 그렇기 때문에 세타2의 값은 각각의 코싸인의 값에 따라서 두개의 복수의 값이 주어지게 되겠습니다
이 두 개 값에 의해서 $\theta_2$가 결과적으로는 이렇게 작은각과 큰각으로 주어질 수 있는데 그렇게 주어졌을 때 이렇게 upper arm과 lower arm의 형태로써 $\theta_2$가 결정되게 되는 것 입니다.
그래서 이렇게 $cos$제2법칙을 이용해서 $\theta_2$는 $arccos$ 이라는 식을 이용해서 결과적으로 다 주어진 $X,Y,l_1,l_2$를 이용해서 구할 수가 있습니다.
이 때 주의해야할 점이 아까 살펴본 바로는 이렇게 Manipulator의 형태가 upper arm과 lower arm의 형태로 배치가 될 수가 있고 두 가지 솔루션을 구할 수가 있다라고 말씀을 드렸는데요. 이렇게 주어지는 이유가 $cos$의 그래프를 그려보면 $cos$의 그래프는 이와 같이 그려지는 것을 여러분들이 확인하실수가 있죠.
그래서 같은 값이더라도 이러한 값과 이러한 값으로 두 가지 솔루션을 얻게 되는 것이죠. 그렇기 때문에 또는 이 값은 마이너스값이라고 볼 수도 있는 것이고요.
그래서 이렇게 $cos$제2법칙을 이용해서 $\theta_2$는 $arccos$ 이라는 식을 이용해서 결과적으로 다 주어진 $x,y,l_1,l_2$를 이용해서 구할 수가 있습니다.
이럴 때 주의해야할 점이 아까 살펴본 바로는 이렇게 Manipulator의 형태가 upper arm과 lower arm의 형태로 배치가 될 수가 있고 이렇게 $\theta_2$를 먼저 결정하고 나면 그 다음으로는 $\theta_1$을 찾아야 합니다.
.jpg)
$\theta_1$의 값을 구할 때 우리는 $sin$법칙을 활용합니다.
$sin$법칙은 삼각형이 이렇게 주어졌을 경우에 마주보는 각과 그리고 그 마주보는 길이, 마주보는 변의 길이를 싸인을 통해서 서로 같은 비율을 가진다는 것을 이용하는 것 입니다.
즉, 이 끼인각이 B고 이 길이가 b 였을 경우에, 이렇게 주어졌을 때 이것들간의 관계는 여기에 주어진 것 처럼 $sin$법칙으로, 변의 길이 분의 그 변을 마주보는 각도에 대한 $sin$값은 서로 모든 세 각과 세 변에 대해서 성립한다는 것을 활용합니다. 조금전에 $\theta_2$를 구했으면 이 삼각형 내에서 이 각도를 구한것과 같은 개념이죠. 그래서 이 각도는 $sin(180 - \theta_2)$라는 값으로 사용할 수가 있습니다.
이 각의 마주보는 이 변의 길이를 $\sqrt {x^2+y^2}$ 즉, 이 변의 길이를 이렇게 정의할 수가 있게 됩니다.
이렇게 된 상태에서 필요로 하는 $\theta_1$을 얻고 싶은건데, $\theta_1$값은 이 $\alpha$, 즉 $x$하고 $y$라는 값이 주어지면 $arctan$에 의해서 구할 수 있는 이 $\alpha$값과 그리고 이 사이에 끼인각을 $\theta_1$에 바라고 했을 경우에 이 두개의 더하기로 이 $\theta_1$을 결정할 수 있게 됩니다.
그러면 이 $\theta_1$을 조금전에 말씀드렸던 이 각의 비율을 활용해서 구한다면 이 마주보는, 이 $\theta_1$에 대한 마주보는 이 길이를 $c$ 또는 $l_2$라고 했을 경우에 이 $sin(\theta_1) \above 1pt l_2$의 값을 이용해서 이러한 방법을 이용해서 이 $\theta_1$에 대한 값을 $\bar \theta_1$에 대한 값을 구할 수 있게 되는 것이죠. 이렇게 $\bar \theta_1$와 $\alpha$에 대한 수식을 정리를 했습니다.
.jpg)
그렇게 얻어진 것을 바탕으로 $\theta_1$은 $arcsin$, 이 수식 그리고 $arctan2$라는 값을 이용을 해서 역시 이 안에서도 보시면 $x,y,l_2$ 전부다 알고 있는 값들 이었고 $\theta_2$라는 값은 바로 이전에 $cos$제2법칙을 이용해서 구한 값이 되겠죠. 그래서 $\theta_2$의 값에 따라서 역시 마찬가지로 $\theta_1$의 값도 두 개가 나올 수 있는 것이죠.
아까 전에 그림을 통해서 설명드렸던 것처럼, $\theta_2$의 값이 이렇게 주어지게 되고 $\theta_2$의 값이 이렇게 두 가지의 솔루션이 나온것과 마찬가지로 만약에 $\theta_2$의 값이 이렇게 +의 값으로 주어지게 되면 이게 $\theta_1$의 값이 되겠고요. 만약에 $\theta_2$의 값이 이와같이 -값으로 주어지게 되면 $\theta_1$의 값은 이렇게 주어지게 되겠죠. 즉 $\theta_2$에 따라서 마찬가지로 $\theta_1$도 두 개의 솔루션을 얻게되는 결과를 볼 수 있습니다.