서울과학기술대학교 김진현교수님의 K-MOOC강좌 Robot Manipulator and Underwater Robot Application을 공부하고 내용을 정리한 것 입니다.
K-MOOC 강좌 주소:
http://www.kmooc.kr/courses/course-v1:SEOULTECHk+SMOOC03k+2019_T3/about
선형 변환(Linear Transformation)
선형 변환(Linear Transformation)
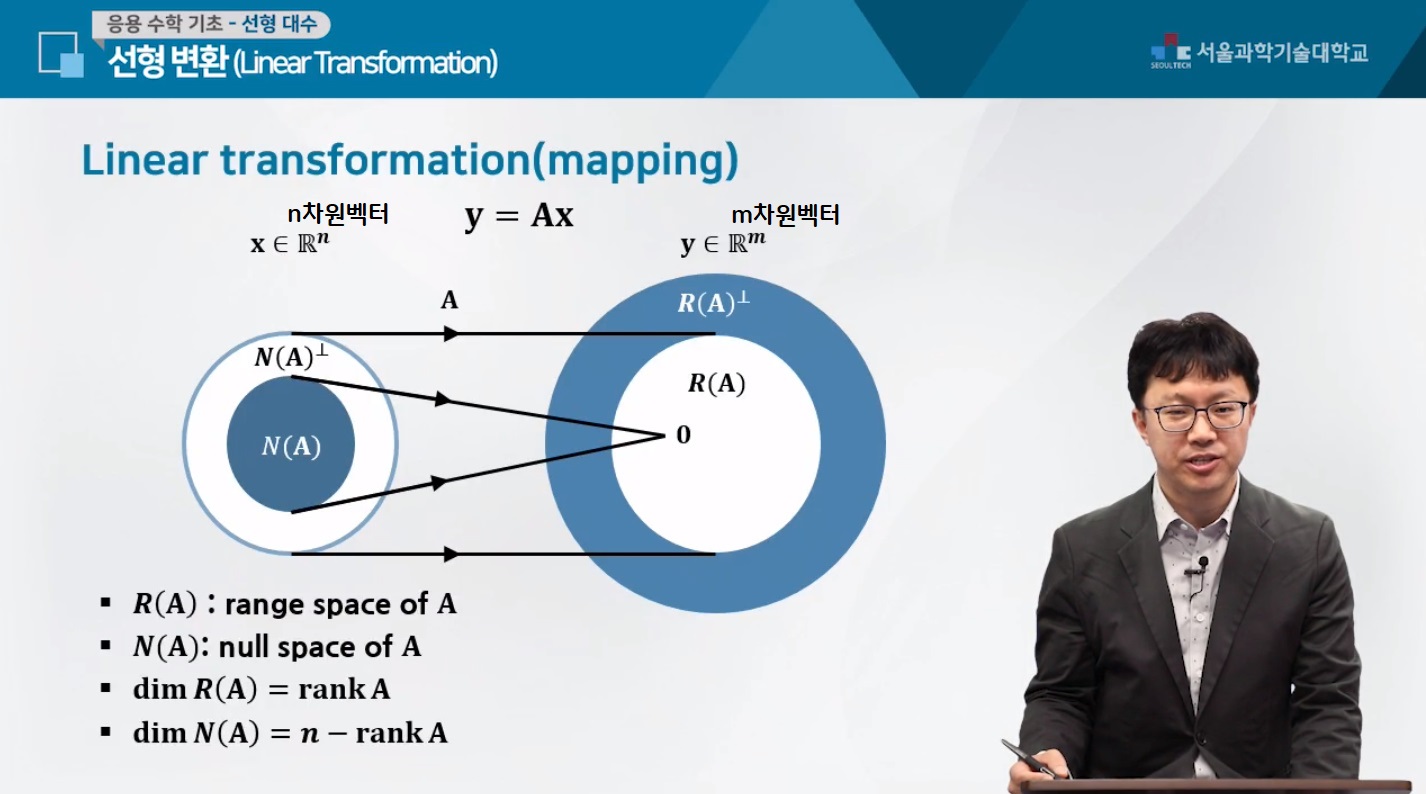
|$x$라고 되어 있는 어떠한 공간에서, $A$라는 행렬을 통해서 $y$라는 공간으로 변환된다, 라는 개념으로 어떤 매트릭스 연산을 설명할 수 있습니다.|
이런 개념이 필요한 이유는, 이어서 기구학에서 살펴볼, 조인트 스페이스와 태스크 스페이스, 즉 관절 공간과 작업 공간에서의 서로간의 속도 변환, 그리고 서로간의 위치 변환 같은 것들을 설명하기 위해서는, 이런 선형변환이라는 것에 대해서 여러분들이 익숙해질 필요가 있습니다.
range space of $A$: 어떠한 매트릭스 $A$가 존재하고, 그 매트릭스 $A$에, Column으로 이루어져 있는, 이 Column들을 가지고 만들 수 있는, Span할 수 있는 공간 전체를 range space라고 합니다.(Column space)
이 레인지 스페이스 이외의 공간, 어떻게 보면 이렇게 만들어진 2차원 공간이라면, 이 2차원 공간과 수직하는 공간을, 레인지 스페이스의 직교공간이다, 라고 말할 수 있습니다.
Range of space를 벗어나 있는 직교공간으로는 어떠한 수를 쓰더라도 이 $A$라는 매트릭스를 통해서는 갈 수가 없게 됩니다.
Null space of $A$: 선형 방정식 $Ax=b$에서 $b$가 zero vector(=Null vector, =0벡터)일때 식을 만족시키는 모든 가능한 해 $x$에 대한 집합이다. 다시 말하면 선형방정식 $Ax=0$의 해들이 이루는 공간, Null Space를 의미한다.
Matrix Norms
.jpg)
p-norm: $Ax=y$임을 이용해 매트릭스가 아닌 벡터로 놈을 정의함
$sup$(상한): 가장 큰 값을 찾는 연산
F-norm(frobenius norm): 각각의 요소들을 전부 제곱을 한후 square root를 취한 norm(L2 norm형태)
의사역행렬(Pseudo-inverse)
.jpg)
|두개의 벡터가 차원이 다를 경우라도 변환은 존재할 수 있는데, 이런 정방행렬이 아닐 경우에는 역행렬이 존재하지 않기 때문에 어떤 역으로 오는 변환하는 설명이 조금 어려울 것입니다.|
.jpg)
의사역행렬(Pseudo-inverse): $A$가 정방행렬이 아닌 경우에 대해서 정의할 수 있는 역행렬의 개념으로 실제 역행렬은 아니지만, 이것은 가상의 역행렬이다.
.jpg)
만약에 m이 n보다 작은 경우, 즉 그런 경우에 full row rank, 즉 row 방향으로 Rank가 전부 다 꽉 차 있을 경우에는, 오른쪽의 pseudo-inverse가 존재하고 오른쪽에만 곱했을 때, identity matrix를 만들 수 있는 성질을 가지고 있다.(right pseudo-inverse)
그런데, 그 중에서 Moore-Penrose pseudo-inverse라는 방법으로 정의되어 있는 역행렬이 가장 널리 사용되고, 가장 많이 사용되고 있는 역행렬, 이 pseudo-inverse에 계산하는 방법이 되겠습니다.
각각 $A$,$A^T$는 각각의 $A$의 Rank와 $A^T$의 Rank는 똑같이 같아지고 2개를 곱했기 떄문에 역시 Rank는 같습니다.
그리고 full row rank이기 때문에, 당연히 역행렬이 존재할 수가 있게된다.
반대로, m이 n보다 큰 경우에는 즉 full column rank를 가진 경우에는, 이번에는 왼쪽에 곱했을 경우에만, $I$를 만들 수 있는 left Pseudo-inverse가 존재합니다.
Pseudo-inverse의 경우 표기를 A^# $A^+$ A^십자가모양등 다양하게 사용된다.
.jpg)
의사역행렬을 이용한 역변환:
어떤 $y=Ax$라고 하는 변환을 생각을 할 수가 있는데, 이런 $y=Ax$에서, 그렇다면 이번에는 $x$라는 것을 거꾸로, $A$라는 어떤 Pseudo-inverse를 통해서, $y$라는 것을 통해서 역변환을 구할 경우 단순하게 $x=A^+y$라고만 하면 되는 게 아니라, 거기에 추가적으로 이와 같은 Null space로 프로젝션시키는 여분의 텀이 존재해야만 정확하게 표현이 가능해집니다.
.jpg)
$A^+=B$라고하면 이 B라는 행렬에 대한 널 스페이스, 그리고 널 스페이스와 직교하는 스페이스, 그 다음에 이 $B$라는 행렬에 대한 Range space, 그 다음에 $B$라는 행렬에 대한 Range space에 직교하는 행렬, 직교하는 스페이스, 이렇게 4가지의 공간이 존재하게 되겠고요, 그래서 결과적으로는 이 Range space, $A^+$의 Null space에 존재하는 놈, 또는 앞서서 연산했던 것과 마찬가지로, 결국에는 Null space에 존재하기 때문에, 전부 다 0으로 수렴하게 됩니다.
그리고 이, $A^+$의 Null space에 존재하는, 이 Null space에 존재하지 않는,
즉 이 Null space와 직교하는 공간에 있는 이러한 인자들은 전부 다 이 $A$라는 $A^+$의 Range space로 전부 다 매칭이 되는 거죠.
그렇다면, 역시 마찬가지로 이 공간을 만들어낼 수 없다는 문제가 생기게 됩니다.
원하는 것은 이 $x$라는 것이 $A$라는 것을 타고, $y$로 갔다가, 다시 $y$를 통해서, $x$로 복구가 되는 과정을 원하는 것이고, $x$ 전체를 만들어내는 것이 우리의 목표인데,
이러한 역변환을 통해서 이 공간, 즉 앞서서 Null space, $A$의 Null space와 직교하는 공간에 있는 점들을 전부 다 만들어 낼 수가 있는데,
Null space 상의, 즉 $A$의 Null space에 존재하는 것들을, 공간을 만들어낼 수가 없게 됩니다.
.jpg)
그래서, 이러한 공간을 만들어내기 위해서, 이와 같이 $I-A^+A$라고 하는, 가상의 새로운 프로젝션(projection)시키는, 변환을 만들어내게 됩니다.
이 변환은, 여기에서는 유의하실 게, $x$에서 $x$로 가는 변환입니다. $y$에서 $x$로 가는 변환이 아닌, $x$에서 $x$로 가는 변환인데, 이 $x$에서 $x$로 가는 변환은, 즉 모든 $x$를 전부 다 Null space로 보내는 변환이 되겠습니다.
그래서 $x$상에 있는 그 모든 원소들을 전부 다 이 Null space로 보내주고 직교하는 것들은 이 Null space에 직교하는 공간들은 전부 0으로 보내는, 변환이 바로 $I-A^+A$라고 하는, 변환이 되겠고요,
이러한 변환을 통해서 앞서 페이지에서 만들어내고 싶었던, $A$라고 하는 것의 Null space에 직교하는 공간을, 만들어낼 수가 없었는데, 이 공간을 이러한 변환을 통해서 만들어낼 수가 있게 되는 겁니다.
그래서 조금 전에 말씀드렸던 것처럼, 선형변환을 통해서, $x$라는 것을 만들어내기 위해서 $A^+$에 $y$를 곱해주고,
그 다음에 $(I-A^+A)k$, 이때 $k$는 $x$하고 같은 크기의 임의의 어떤 벡터가 되겠고요,
이러한 변환을 통해서 온전하게 $x$를 다시 변환을 통해서 만들어낼 수가 있게 되는 겁니다.
이 개념이 나중에 기구학에서, 여러분들이 관절공간과, 그리고 작업 공간을 왔다갔다 하는 데에 있어서 꼭 필요한 개념이 되겠습니다.