CS 285 at UC Berkeley을 보고 정리한 글입니다.
Definitions
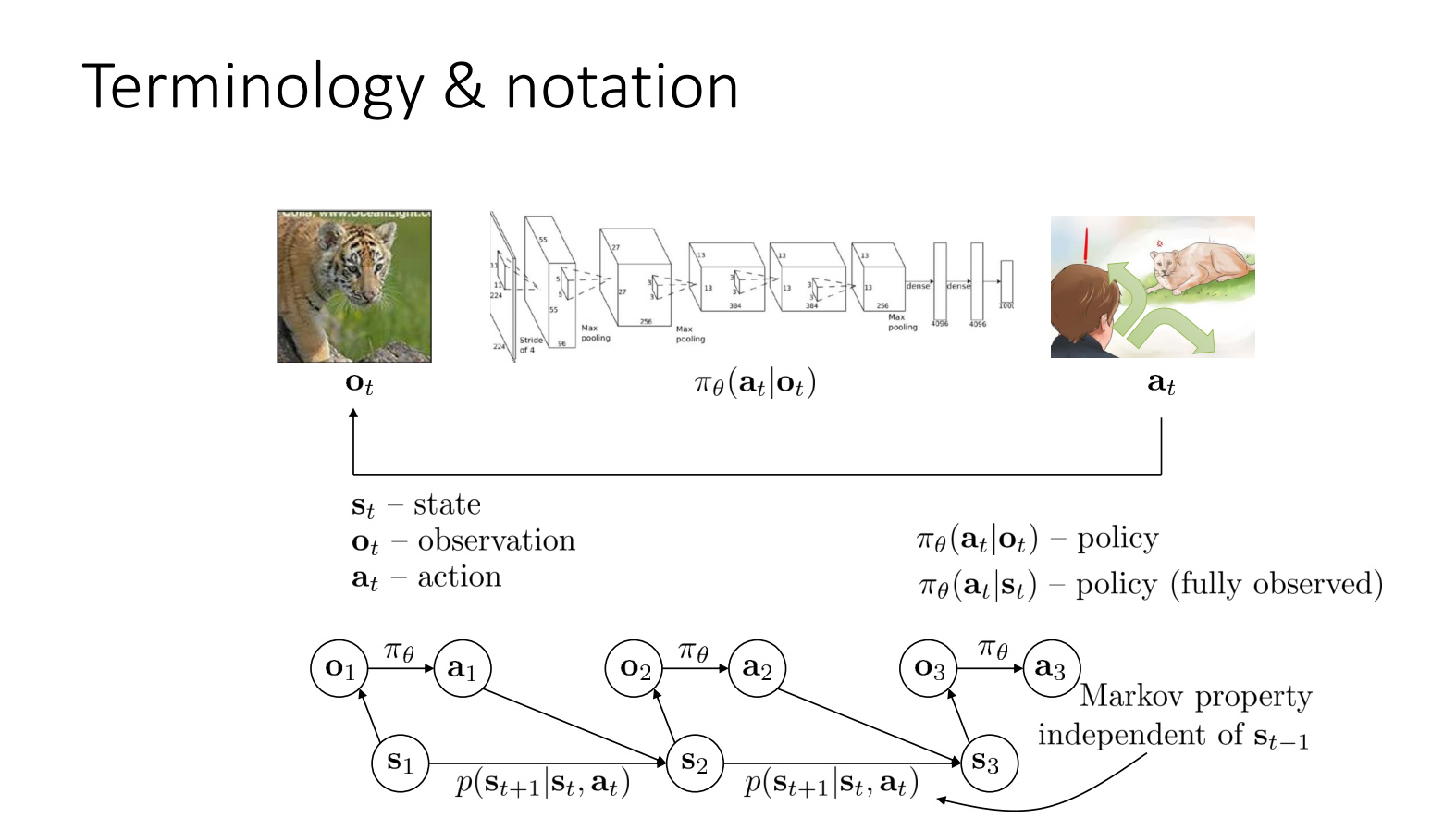
- 강화학습의 목적은 $\theta$를 찾는 것이 목적이다.
- state는 markov property를 만족하고 observation은 만족하지 않는다.
- $\pi_{\theta} \mathbf (a_t|o_t)$는 partially observed라고 하고 $\pi_{\theta} \mathbf (a_t|s_t)$ fully observed라 한다.
- POMDP(Partially observable Markov decision process)와 Fully observed MDP가 있는데 일반적으로 Fully observed MDP로 가정한다.
behavior cloning
.jpg "cs285 paper")
- 전문가로부터 data(observation,action)을 수집해서 supervised learning을 사용한다.
- 일반적으로 behavior cloning은 잘 안되지만 DAgger를 사용하면 성능이 향상된다.
reward function
.jpg "cs285 paper")
- $\mathbf r(s,a)$(reward function): 어떤 행동이 좋고, 어떤 행동이 나쁜가?에 대한 기준
- $s,{\mathbf a},r(s,a),p(s’|s,a)$ (transition probability)로 이뤄진 것을 Markov decision process라 한다.
Markov chain
.jpg "cs285 paper")
- $\mathcal{M} = {\mathcal{S,T}}$
- 아직 RL은 아니다.(no agency,no action)
- $\mathcal{S}$ - state space
- states $s \in \mathcal{S}$(discrete or continuous)
- $\mathcal{S}$: set of valid state
- $s$:state
- $\mathcal{T}$ - Transition operator
- $p (s_{t+1}|s_t)$
- why “operator”?
- Discrete space에서 $\mathcal{T}$ linear operator처럼 쓰이기 때문
- let $\mu_{t,i} = p(s_t = i) \vec{\mu_t}$ is a vector of probabilites
- $\mu_{t,i}$: time step $t$에서 주어진 state $i$일 확률
- let $\mathcal{T}_ {i,j} = p(s_{t+1} = i|s_t = j)$ then $\vec{\mu_{t+1}} = \mathcal{T}\vec{\mu_t}$
- $\mathcal{T}_{i,j}$ -> $N\times N$ matrix($N$:가능한 state 개수)
- 다음 step의 state 확률을 $\mathcal{T}$와 현재 step의 state 확률의 곱으로 구할 수 있다.
- $\vec{\mu_{t+1}} = \mathcal{T}\vec{\mu_t}$이 linear operator 처럼 행동
- stationary distribuition 때 중요
Markov decision process
.jpg "cs285 paper")
.jpg "cs285 paper")
- $\mathcal{M} = {\mathcal{S,A,T,r}}$
- $\mathcal{S}$ - state space
- states $s \in \mathcal{S}$(discrete or continuous)
- $\mathcal{A}$ - action space
- actions $a \in \mathcal{A}$(discrete or continuous)
- $\mathcal{O}$ - observation space
- observations $o \in \mathcal{O}$(discrete or continuous)
- $\mathcal{T}$ - Transition operator(Tensor!)
- action과 state를 가지고 있기에 Tensor이다.($p (s_{t+1}|s_t,a_t)$)
- let $\mu_{t,j} = p(s_t = j)$
- let $\xi_{t,k} = p(a_t = k)$
- let $\mathcal{T}_ {i,j,k} = p(s_{t+1} = i|s_t=j,a_t=k)$
- $\mu_{t+1,i} = \sum_{j,k} \mathcal{T}_ {i,j,k}\mu_{t,j}\xi_{t,k}$(linear operator)
- $r$ - reward function
- $r : \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}$(scalar field)
- $r(s_t,a_t)$ - reward
Partially observed Markov decision process
.jpg "cs285 paper")
- $\mathcal{M} = {\mathcal{S,A,O,T,\varepsilon,r}}$
- $\mathcal{S}$ - state space
- states $s \in \mathcal{S}$(discrete or continuous)
- $\mathcal{A}$ - action space
- actions $a \in \mathcal{A}$(discrete or continuous)
- $\mathcal{O}$ - observation space
- observations $o \in \mathcal{O}$(discrete or continuous)
- $\varepsilon$ - emission probability(operator)
- $p(o_t|s_t)$
- $r$ -reward function
- $r : \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}$
The goal of reinforcement learning
.jpg "cs285 paper")
Goal: reward를 최대로하는 policy 찾기(learn $\theta$)
- 항상 policy가 explicit 하지 않지만 지금은 explicit
$p_\theta(s_1,{\mathbf a_1},\dots,s_T,{\mathbf a_T}) = p(s_1) \prod_{t=1}^T\pi_\theta({\mathbf a_t}|s_t)p(s_{t+1}|s_t,{\mathbf a_t})$
- finite horizon으로 가정
- $p_\theta(s_1,{\mathbf a_1},\dots,s_T,{\mathbf a_T}) = p_\theta(\mathcal{T})$ (joint probability distribution, $\mathcal{T}$는 trajectory)
- $s_{t+1}$는 보통 모른다.
$\theta^\star = \arg \max_{\theta}E_{\mathcal{T}\sim p_\theta(\mathcal{T})}[\sum_t r(s_t,{\mathbf a_t})]$
- 우리는 모든 time step마다 reward가 최대가 되길 원한다. 그래서 모든 time step에 대해 reward를 더한다.
- $s_t,{\mathbf a_t}$는 $\mathcal{T}\sim p_\theta(\mathcal{T})$에 대해 uncertain(randomly distributed)하기에 기댓값을 사용($\sum_{x-p(x)}[f(x)]=\int p(x)f(x)dx)$)
- 이 식은 policy의 목적이기에 action을 알려주지 않아서 기댓값은 가능한 모든 state와 action의 sequence를 고려해야한다.
.jpg "cs285 paper")
.jpg "cs285 paper")
$\theta = \arg \max_{\theta}E_{\mathcal{T}\sim p_\theta(\mathcal{T})}[\sum_t r(s_t,{\mathbf a_t})]$
- distribution이 MDP를 만족하지 않아도 $\pi_\theta({\mathbf a}|s)$가 정해지면 $s$와 $\mathbf a$의 합쳐짐으로 얻어진 augmented state space에서 markov chain으로 볼수있다.
$p((s_{t+1},\mathbf{a_{t+1}})|(s_t,\mathbf{a_t}))) = p(s_{t+1}|s_t,\mathbf{a_t})\pi_\theta(\mathbf{a_{t+1}}|s_{t+1})$
Finite horizon case: state-action marginal
.jpg "cs285 paper")
- $\theta^\star = \arg \max_{\theta}E_{\mathcal{T}\sim p_\theta(\mathcal{T})}[\sum_t r(s_t,{\mathbf a_t})]$
- $\mathcal{T}$를 $s$와 $a$의 pair로 변경
- $p_\theta(s_t,\mathbf{a}_t)$(state-action marginal)
- time step $t$에서의 state와 action의 marginal distribution
Infinite horizon case: stationary distribution
.jpg "cs285 paper")
what if $T = \infty$?
$p(s_t,\mathbf{a_t})$가 stationary distribution으로 수렴 한다면(항상은 아니지만 일반적으로 수렴) $\begin{pmatrix} s_{t+1} \ a_{t+1} \end{pmatrix} = \mathcal{T}^k \begin{pmatrix} s_{t} \ a_{t} \end{pmatrix}$(state-action transition operator)을 이용해서 $\mu = \mathcal{T}\mu$로 나타낼 수 있다.
$\mu$: vector of probabilities state action pair
$\mu = \begin{bmatrix} p(s_1) \cr p(s_2) \cr \vdots \cr p(s_N) \end{bmatrix} \ \ \text{(regular markov chain) } \mu = \begin{bmatrix} p(s_1,a_1) \cr p(s_1,a_2) \cr p(s_1,a_M) \cr p(s_2,a_1) \cr \vdots \end{bmatrix} \ \ ( \text{markov chain over} s \ \ \text{and} \ \ a)$
not change distribution $\ne$ not change state
$(\mathcal{T} - I)\mu = 0$
- $\mu$는 $\mathcal{T}$의 eigenvalue가 1인 eigenvector이다.
- 특정 조건(ergodicity - 모든 state action pair가 reachable)을 만족하면 수렴한다.
.jpg "cs285 paper")
- $\theta^\star = \arg \max_{\theta} \frac{1}{T} \sum^T_{t=1}E_(s_t,\mathbf{a_t})\sim p_\theta(s_t,\mathbf{a_t})[r(s_t,\mathbf{a_t})] \rightarrow E_{(s,\mathbf{a})\sim p_\theta(s,\mathbf{a})}[r(s,\mathbf{a})]$
- $T$가 무한대으로 가면 이전 공식이 무한대로 가기 때문에 $\frac{1}{T}$을 추가함(undiscounted average return)
- $\sum$이 $E$에 압도되어 결국 $E_{(s,\mathbf{a})\sim p_\theta(s,\mathbf{a})}[r(s,\mathbf{a})]$이 된다.
.jpg "cs285 paper")
RL에서 목적은 주로 expectation만을 고려한다.
그림처럼 도로위에 있으면 reward +1 이고 그외에는 -1이라 하자
- reward function은 not smooth, not differentiable하다.
- 하지만 expectation을 추가하면 $\theta$ ($pi_\theta(\mathbf{a}=fall)=\theta$, distribution) 안에서는 smooth 해진다.($\theta * (-1) + (1-\theta)*1$이므로)
Algorithms
The anatomy of RL algorithm
.jpg "cs285 paper")
- ( sample 생성(즉 policy대로 agent 행동, collect data) )
- ( Fit a model/ estimate the return(evaluation step, policy를 바꾸지 않고 평가한다.) )
- ( improve the policy(policy를 업데이트한다.) )
.jpg "cs285 paper")
- ( 위 그림에서 trajectories )
- ( evaluate reward function(나쁜결과는 probability 낮춘다))
- ( $\theta \leftarrow \theta + \alpha \nabla_{\theta}J(\theta)$(gradient descent) )
.jpg "cs285 paper")
- Model based RL
- ( $s_t$와 $\mathbf a_t$가 input으로 받고 output으로 $s_{t+1}$를 출력하는 $f_{\phi}$를 학습한다.(fitting neural net) )
- ( $\pi_\theta(s_t)$를 학습 시키기 위해 $f_{\phi}$와 $r$을 통해서 backprop한다. )
.jpg "cs285 paper")
- Which parts are expensive?
- ( 실제 로봇이나 차등은 현실 시간과 동일하므로 오래 걸리지만 MuJoCo같은 시뮬레이션은 빠르다. )
- ( reward를 계산하는 것은 빠르지만 neural net을 사용하면 느리다.(알고리즘에 따라 다르다.) )
- ( gradient step같은경우 빠르지만 backprop은 느리다.(알고리즘에 따라 다르다.) )
How do we deal with all these expectations?
.jpg "cs285 paper")
$E_{\mathcal{T}\sim p_\theta(\mathcal{T})}[\sum_t r(s_t,\mathbf a_t)]$
$ E_{s_1 \sim p(s_1)} [E_{\mathbf{a}_1\sim \pi (\mathbf {a} _1|s_1)} [r(s_1,{\mathbf a}_1)+\ |s_1]] $
- state $s_1$에서 action $a_1$을 한다.
$ E_{s_{1} \sim p\left(s_{1}\right)}\left[E_ {\mathbf{a}_ {1} \sim \pi\left(\mathbf{a}_ {1} | \mathbf{s}_ {1}\right)}\left[r\left(\mathbf{s}_ {1}, \mathbf{a}_ {1}\right)+E_{\mathbf{s}_ {2} \sim p\left(\mathbf{s}_ {2} | \mathbf{s}_ {1}, \mathbf{a}_ {1}\right)}[ | \mathbf{s}_ {1}, \mathbf{a}_ {1}\right] | \mathbf{s}_{1}]\right] $
- transition probability distribution $p(s_2|s_1,\mathbf{a_1})$에 따라 state $s_2$로 가고 action $a_2$를 한다.
$ E_{s_{1} \sim p\left(s_{1}\right)}\left[E_ {\mathbf{a}_ {1} \sim \pi\left(\mathbf{a}_ {1} | \mathbf{s}_ {1}\right)}\left[r\left(\mathbf{s}_ {1}, \mathbf{a}_ {1}\right)+E_{\mathbf{s}_ {2} \sim p\left(\mathbf{s}_ {2} | \mathbf{s}_ {1}, \mathbf{a}_ {1}\right)}\left[E_{\mathbf{a}_ {2} \sim \pi\left(\mathbf{a}_ {2} | \mathbf{s}_ {2}\right)}\left[r\left(\mathbf{s}_ {2}, \mathbf{a}_ {2}\right)+\ldots | \mathbf{s}_ {2}\right] | \mathbf{s}_ {1}, \mathbf{a}_ {1}\right] | \mathbf{s}_{1}\right]\right] $
expectation이 많지만 markov property때문에 각각 1,2개의 condition만을 가진다.(convenient 해진다.)
- ex) $E_ {\mathbf{a}_ 2 \sim \pi (\mathbf{a}_ {2} | \mathbf{s}_{2})}$는 $s_2$만을 condition으로 받음
$ r (\mathbf{s}_ {1}, \mathbf{a}_ {1} )+E_{\mathbf{s}_ {2} \sim p (\mathbf{s}_ {2} | \mathbf{s}_ {1}, \mathbf{a}_ {1} )} [E_{\mathbf{a}_ {2} \sim \pi (\mathbf{a}_ {2} | \mathbf{s}_ {2} )} [r (\mathbf{s}_ {2}, \mathbf{a}_ {2} )+\ldots | \mathbf{s}_ {2} ] | \mathbf{s}_ {1}, \mathbf{a}_ {1} ] | \mathbf{s}_{1} ]]$를 안다면?
- time step $T$까지 기다릴 필요 없이 바로 policy를 앞으로의 보상에 맞게 학습할 수 있을 것이다.(drastically simplify)
$Q(s_1,\mathbf{a_1}) = r(\mathbf{s}_ {1}, \mathbf{a}_ {1})+E_{\mathbf{s}_ {2} \sim p(\mathbf{s}_ {2} | \mathbf{s}_ {1}, \mathbf{a}_ {1})}[E_{\mathbf{a}_ {2} \sim \pi(\mathbf{a}_ {2} | \mathbf{s}_ {2})}[r(\mathbf{s}_ {2}, \mathbf{a}_ {2})+\ldots | \mathbf{s}_ {2}] | \mathbf{s}_ {1}, \mathbf{a}_ {1}]$
$E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t=1}^{T} r\left(\mathbf{s}_ {t}, \mathbf{a}_ {t}\right)\right]=E_{\mathbf{s}_ {1} \sim p\left(\mathbf{s}_ {1}\right)}\left[E_{\mathbf{a}_ {1} \sim \pi\left(\mathbf{a}_ {1} | \mathbf{s}_ {1}\right)}\left[Q\left(\mathbf{s}_ {1}, \mathbf{a}_ {1}\right) | \mathbf{s}_{1}\right]\right]$
- 만약 모든 $s$, $a$에 대해서 $Q(s,a)$를 안다면 $\pi$를 쉽게 바꿀 수 있다.
- ex) 만약 ${\mathbf a_1} = \arg \max_{\mathbf a_1} Q(s_1,{\mathbf a_1})이면 $\pi\theta (\mathbf{a} _1|s_1) = 1$ 이다.(나머지 확률이 0이라)
- $Q$도 $\pi$에 영향을 받지만 지금은 고려하지 않는다.(나중에 트릭으로 해결)
- 만약 모든 $s$, $a$에 대해서 $Q(s,a)$를 안다면 $\pi$를 쉽게 바꿀 수 있다.
Q-function and value function
.jpg "cs285 paper")
- Q-function(quality function): $s_t$에서 $\mathbf a_t$를 했을때 앞으로 받을 전체 reward의 합
- $Q^{\pi}(s_t,{\mathbf a_t}) = \sum\nolimits^T_{t’=t} E_{\pi_\theta}[r(s_{t’},{\mathbf a}_{t’})|s_t,{\mathbf a_t}]$
- value function: $s_t$로부터 앞으로 받을 전체 reward의 합
- $V^{\pi}(s_t) = \sum \nolimits_{t’=t}^{T} {E}_ {\pi_{\theta}} [ r(s_{t’},{\mathbf a}_{t’}) | s_t]$
- $V^{\pi}\left(\mathbf{s}_ {t}\right)=E_{\mathbf{a}_ {t} \sim \pi\left(\mathbf{a}_ {t} | \mathbf{s}_ {t}\right)}\left[Q^{\pi}\left(\mathbf{s}_ {t}, \mathbf{a}_{t}\right)\right]$
.jpg "cs285 paper")
Idea1: $\pi$와 $Q^\pi(s,{\mathbf a})$를 안다면 $\pi$를 improve 할수있다.
- 만약 ${\mathbf a} = \arg \max_{\mathbf a} Q^\pi(s,{\mathbf a})$라면 ${\pi}’({\mathbf a}|s) = 1$으로 맞춘다.
- 그러면 ${\pi}’$는 적어도 $\pi$보다 좋거나 같아진다.
Idea2: good action $\mathbf a$의 확률 증가시키기 위해 gradient 계산
- 만약 $Q^\pi(s,{\mathbf a}) > V^{\pi}(s)$면 $\mathbf a$는 평균보다 더 좋다.($V^{\pi}(s_t) = \sum\nolimits_{t’=t}^{T} {E}_ {\pi_{\theta}} [ r(s_{t’},{\mathbf a}_{t’}) | s_t]$이기 때문)
- $Q^\pi(s,{\mathbf a}) > V^{\pi}(s)$인 $\mathbf a$의 확률을 크게하게 $\pi({\mathbf a}|s)$로 바꾼다.(actor critic)
.jpg "cs285 paper")
Types of RL algorithms
.jpg "cs285 paper")
- Objective: $\theta^\star = \arg \max_{\theta}E_{\mathcal{T}\sim p_\theta(\mathcal{T})}[\underset{t}\sum r(s_t,\mathbf a_t)]$
- Policy gradients: 위 objective를 집접적으로 미분
- Value-based: optimal policy의 Q-function or value function을 추정(no explicit policy)
- Actor-critic: 현재 policy의 Q-function or value function을 추정, policy를 향상시키기 위해 사용(combination Policy gradients and Value-based)
- Model-based RL: transition model 추정, 그리고
- planning을 위해 모델사용(no explicit policy)
- policy 향상을 위해 사용
- Something else
.jpg "cs285 paper")
.jpg "cs285 paper")
plan하기 위해 모델 사용(no explicit policy)
- trajectory 최적화/ 최적 제어(우선적으로 continuous space) - 필수적으로 action을 최적화하기 위해 backpropagation
- discrete action space에서 discrete planning - e.g., Monte Carlo tree search
Backpropagate gradient into the policy
- 동작하기 위해 몇가지 트릭 필요
Value function을 배우기 위해 모델 사용
- Dynamic programming
- Generate simulated experience for model-free learner(Dyna)
.jpg "cs285 paper")
.jpg "cs285 paper")
.jpg "cs285 paper")
Tradeoffs
Why so many RL algorithms
.jpg "cs285 paper")
- Different tradeoffs
- Sample efficiency(sample collection time)
- stability & ease of use(reliable)
- Different assumptions
- Stochastic or deterministic?
- Continuous or discrete?
- Episodic or infinite horizon?
- Different things are easy or hard in different settings
- Easier to represent the policy?(enviornment의 물리법칙이 복잡하지만 optimal behavior의 패턴은 단순)
- Easier to represent the model?(ex. chess)
sample efficiency
.jpg "cs285 paper")
- Sample efficiency = 좋은 정책을 얻기 위해서 얼마나 많은 샘플이 필요한가?
- 가장 중요한 질문: Off policy 알고리즘 인가?
- Off policy: policy에서부터 새로운 샘플 생성없이 policy를 향상할 수 있다.
- On policy: policy가 조금이라도 변할 때마다 새로운 sample을 생성해야 한다.
.jpg "cs285 paper")
- 왜 덜 efficient한 알고리즘을 사용하는가?
- simulation power가 적게 들면, less efficient하더라도 더 나은 성능을 위해 많은 sample을 얻어서 학습하는 것이 효율적일 수 있다.
stability and ease of use
.jpg "cs285 paper")
- 수렴하는지, 어디에 수렴하는지, 항상 수렴하는지에 대한 이슈다.
- supervised learning에서는 gradient descent를 사용하기 때문에 대개 수렴하지만, RL에서는 대체로 gradient descent를 사용하지 않는다.
- Q-learning: fixed point iteration. converge가 보장되지 않는다.
- Model-based RL: model이 reward에 대해 최적화되는 것이 아니다.
- Policy gradient: gradient descent 보통 least efficient .(but stability)
.jpg "cs285 paper")
Value function fitting
- 가장 좋을때, error of fit을 최소화한다.(Bellman error)
- expected reward와 같지 않다.(better fit for value function $\ne$ better policy)
- 최악의 경우, 최적화 되지않는다.
- 많은 유명한 deep RL value fitting 알고리즘은 비선형의 경우 converge한다고 장담할 수 없다.
- 직접적으로 expected reward를 최적화 하지않는다.
- 가장 좋을때, error of fit을 최소화한다.(Bellman error)
Model-based RL
- model이 error of fit를 최소화한다.
- 수렴한다.
- better mode = better policy라 보장할 수 없다.
- model이 error of fit를 최소화한다.
Policy gradient
- 유일하게 실제로 true objective를 gradient descent(ascent)를 사용한다.
assumptions
.jpg "cs285 paper")
- full observability
- 일방적으로 value function fitting에서 가정된다.
- recurrence를 추가하여 완화할 수 있다.
- episodic learning
- 주로 pure policy gradient에서 가정된다.
- 몇가지 model-based RL에서 가정된다.
- continuity or smoothness
- 몇가지 continuous value function learning 방법에서 가정된다.
- 몇가지 model-based RL에서 가정된다.
.jpg "cs285 paper")