Double DQN

작성일 Edited on In 댓글:

Double DQN

기존의 Q-Learning Algorithm은 특정 조건에서 Q-value를 Overestimate(과평가)되어 좋은 성능을 보이지 못했다.

보상받을 값에 따라서 다음 행동이 결정되는데, 잘못된 행동에 대한 Q-value가 과평가되면 잘못된 방향으로 학습이 진행될 수 있다.

Q-Learning은 estimated된 Q-value에 대한 maximization step이 존재하여 비현실적인 Q-value를 통해 학습하게 된다.

기존의 Q-Learning은 어떤 상태($s’$)에서 취할 수 있는 행동들 중에서 maximum Q-value를 구하는 것을 목표로 학습을 진행한다.

물론 학습을 하다보면 부정확한 value로 estimate되는 것은 당연하다. 만약 모든 값들이 균등하게 over-estimate된다면 이것은 문제가 되지 않으며, 심지어 원하는 값에 대해 overestimate되는 것은 때로 좋은 결과를 불러일으킨다. 그러나 overestimate가 일정하게 되지 않고, 우리가 학습하기를 원하는 값에서 발생되지 않는다면 Policy에 안좋은 영향을 미치게 된다.

Double Q-learning

  • Q-Learning은 Action Select와 Action Evaluate을 위해 같은 $\theta$를 사용 -> Overestimation 발생
    $$ Y_t^Q = R_{t+1} + \gamma max_{a} Q (s_{t+1}, a; \theta_{t}) $$
  • 위의 식을 select와 evaluation을 명확히 하기 위해 아래와 같이 변형할 수 있다.
    $$ Y_t^Q = R_{t+1} + \gamma Q(S_{t+1}, argmax_{a} Q (s_{t+1}, a; \theta_{t}); \theta_t) $$
  • 그리고 Double Q-Learning에서는 아래와 같이 selection과 evaluation을 분리하여 표현한다.
    $$ Y_t^Q = R_{t+1} + \gamma Q(S_{t+1}, argmax_{a} Q (s_{t+1}, a; \theta_{t}); \theta’_t) $$
    • $\theta_t$는 argmax에서 action을 선택하고,$\theta’_t$는 policy를 evaluate하는데 2개의 weights는 서로 switching하며 update된다.

Double DQN

DQN

  • DQN에서도 Overestimation이 존재하기에 식을 위와같이 변경

Result

DQN

$Q_*$: true value(보라선), $Q_t$: single action에 대한 approximation(초록선), sampled states(초록 점들)

  • 첫번째와 두번째 그래프는 sampled states도 맞추지 못했는데 이는 estimation function의 차수가 낮아 충분히 flexible 하지 않기 때문이다.

  • 세번쨰 그래프는 충분히 flexible 하지만 unsampled states에서의 정확성은 떨어진다.

    • 특히 왼쪽에 sampled states 거리가 다른 states보다 멀어서 더 큰 estimation error를 만들었다.

  • 이렇게 특정 순간에 우리가 제한적인 데이터만을 지니는 것이 실제 학습할 때의 환경과 같고 Estimation Error는 실제 학습을 진행할 때 자주 발생하게 된다.

DQN

초록색 그래프: 모든 행동에 대한 estimated action-value, 검은색 그래프: 초록색 그래프중 maximum값

  • max를 취했을 때 Overestimation이 발생한는 것을 볼 수 있다.

DQN

주황색 그래프: Maximum Estimation Function – True Function
파란색 그래프: Double Q Estimation Function – True Function

  • 주황색 그래프의 경우 upward bias을 지니고 있어 항상 양수이다.
  • 파란색 그래프의 경우 평균적으로 거의 0에 근접하다.

DQN

  • 첫번째 열과 두번째 열은 True Value Function만을 다르게 한 것 -> Overestimation이 특정 구조에 종속된 것이 아니라는 것

  • 두번째 열과 세번째 열은 Function approximation의 flexibility가 다름

    • row2는 flexibility가 낮아서 True Value에서도 정확한 값을 갖지 않음
    • row3는 flexibility가 높지만 주어진 True Value거리가 먼 경우에서 정확한 값을 갖지 않음

  • 이렇게 시작되는 Overestimation은 계속해서 propagate되고, 상황은 계속해서 악화됨

DQN

  • DQN의 경우 Overestimation이 발생하면서 Score가 하락함

Dueling DQN

DQN

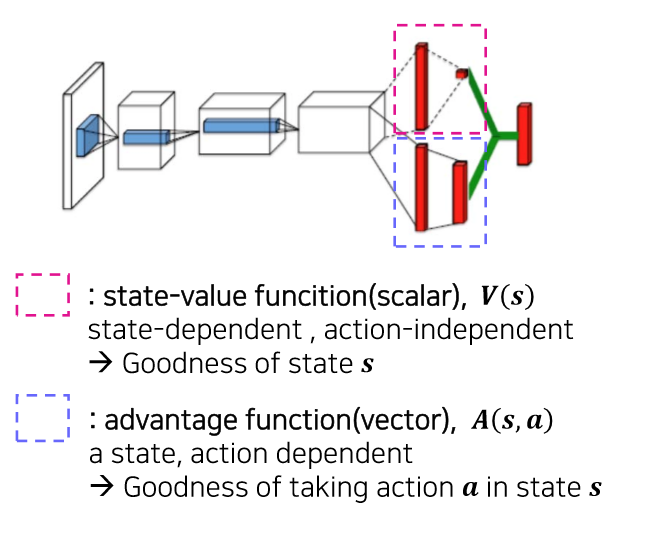
  • 위 stream은 State-value function으로서 scalar 값을 받게 됩니다. 즉, State s가 얼마나 좋냐를 측정하게 되는데 이는 Environment내에서 상대적인 값으로 봐야한다.
    • ex) 7.8이니까 좋다, 라고 말할 수 없고, 이전 상태에서는 5이고 지금 상태는 7이니 이전 상태보다 state value가 높다 라고 해석해야 한다.
  • 아래 stream은 advantage function로 특정 action이 평균 action의 value보다 얼마나 좋은지, 나쁜지를 판단할 수 있는 함수이며 state에 dependent하다.

DQN

  • 마지막 부분은 $V(s) + A(s, a)$로 계산이 됩니다. $V(s)$는 Scalar이고 $A(s, a)$의 action에 대한 vector인데, $V(s) + A(s, a)$를 계산할때에 $V(s)$ 를 action수 만큼 동일하게 복사하여 더해준다.

  • 하지만 이렇게 하면 identifiability 문제가 발생한다.($Q(s,a)$가 주어질떄 $V(s)$와 $A(s,a)$를 찾지 못함, back propagation하는데 문제 발생)

DQN

  • 이 문제의 해결방법은 $A$를 0으로 만들면 되서 위와 같이 식을 바꾸면 된다.

DQN

agent가 앞으로의 reward를 얻기 위해 어디에 관심을 두는지를 표시한 그림

  • 위 그림을 보면 지평선 끝에 차 한대가 작게 있는 것을 볼 수 있다. 먼저, value stream 관점에서는 앞으로의 reward를 최대화 하기 위해서 agent는 score와 멀리 있는 차(장애물) 그리고 차를 피하기위해 가야할 길에 집중한다.

    • advantage stream 관점에서는 집중하지 않는다. 왜냐하면 당장에 action을 취하지 않아도 어차피 차는 나아가고 score는 쌓이고 있기 때문이다.

  • 아래 그림을 보면 차와 다른 차들이 매우 가깝다. 그렇기 때문에 value stream 입장에서는 우리가 계속 score를 쌓기 위해 장애물들을 피해 나아가야할 곳에 집중한다.

    • advantage stream을 보면 당장에 action을 취하지 않으면 reward를 얻는데 영향을 주기 때문에 이때는 앞에 있는 차에 신경을 써서 action을 취해야한다.

  • normal DQN에서는 agent가 state에서 각 action에 대한 Q-value를 계산해야 하지만 value function이 좋지 않을 때, 즉, state가 dangerous하거나 reward를 얻기에 좋지 않은 state에서도 Q-value를 계산해봐야하고, state에서 할 수 있는 모든 action들이 나쁜결과를 초래하더라도 계산해봐야한다.

    • 이렇게 Q-learning을 두 가지 stream으로 dualing하면, agent가 state마다 action을 해보면서 그 결과를 학습하지 않아도 어떤 state가 valuable한지 알 수 있다.

참고 자료