CS285 Fa19 Deep Reinforcement Learning, Decision Making, and Control

CS 285 at UC Berkeley을 보고 정리한 글입니다.

Terminology & notation

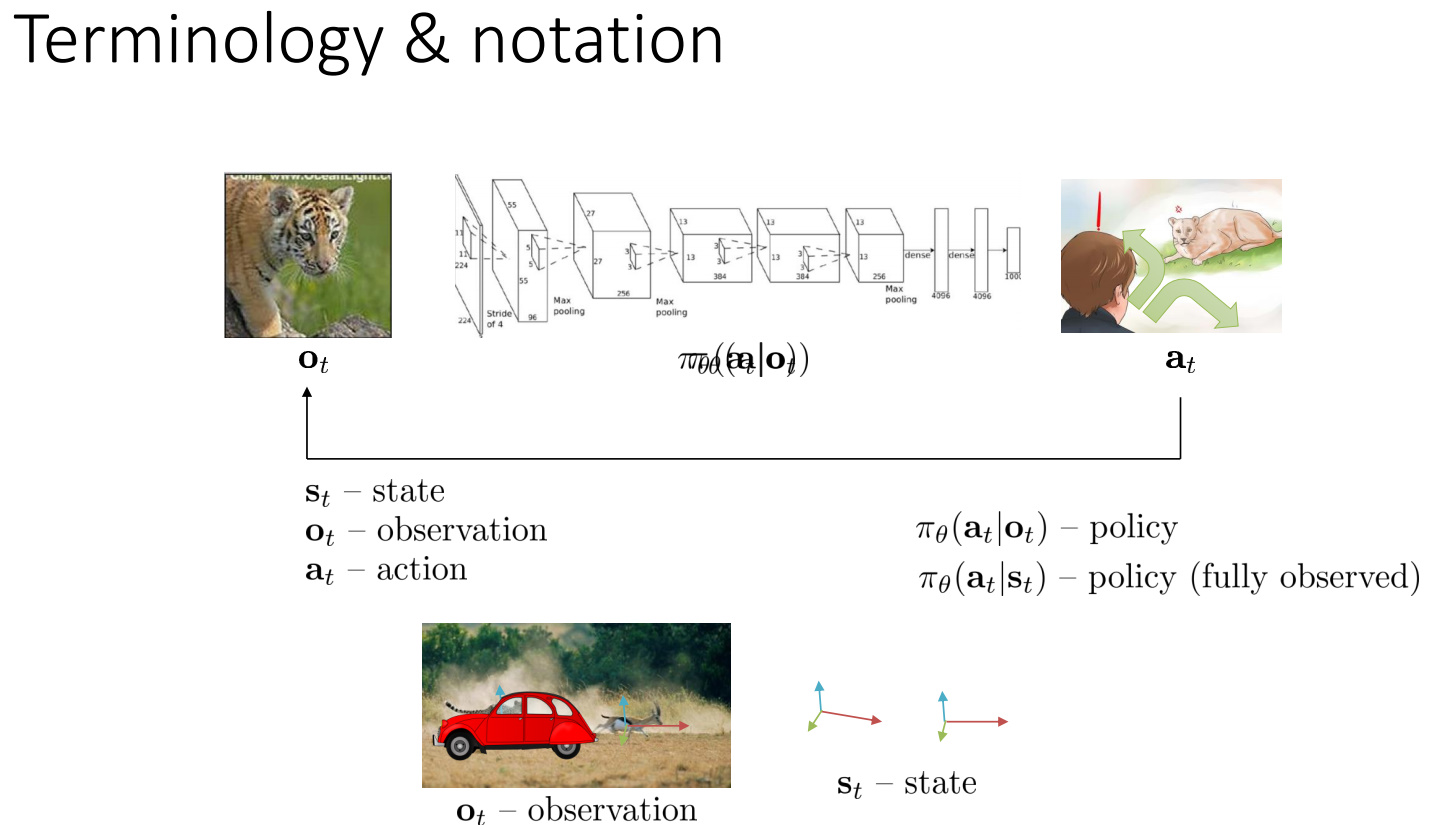
image classification에서는 input으로 image로 받고 output으로 class이지만

순차적 의사결정 문제(sequential decision making problem)에서는 아래첨자에 time step $t$가 추가 되고 output이 $\bf a_t$(action)이 된다. 그리고 순차적 의사결정 문제는 action이 observation($\bf o_t$)에 영향을 끼친다.

$\pi_{\theta} \bf (a_t|o_t)$(policy)은 $o_t$가 주어졌을 때 $a_t$의 확률분포이다.

observation 과 state의 차이

observation($o_t$)는 input 이미지로 볼 수 있고 state($\bf s_t$)는 치타의 상태와 가젤의 상태(environment의 모든 정보)라 할 수 있다. 그래서 위 그림같이 이미지에서 자동차가 치타를 가리면 observation에서는 치타의 정보를 알 수 없지만 state는 알 수 있다.($\pi_{\theta} \bf (a_t|o_t)$는 partially observed라고 하고 $\pi_{\theta} \bf (a_t|s_t)$ fully observed라 한다.)

$\bf p(s_{t+1}|s_t,a_t)$: state $\bf s_t$에서 action $\bf a_t$를 취했을때 $\bf s_{t+1}$로 갈 확률

이러한 성질은 markov chain에서 보면 위 그림과 같다. 여기서 $\bf s_t$에서 $\bf s_{t+1}$로 갈때 $\bf s_{t-1}$은 이와 독립적이다.(future은 past에 독립) 이를 Markov property라고 한다.

위와 같은 그래프가 형성되기 위해서는 state가 필요한데 그 이유는 observation은 markov property를 만족하지 않기 때문이다.

ex) 위 치타와 차 예시를 보면 $\bf o_{t-1}$를 차가 치타를 가리기 전 $\bf o_t$를 차가 치타를 가린 경우 $\bf o_{t+1}$를 차가 지나간 후라면 $\bf o_{t+1}$는 $o_{t-1}$의 정보를 알지 못하면 알 수 없기에 markov property를 따르지 않는다.

가끔 state를 $\scr{x_t}$로 action을 $\bf u_t$로 나타내기도 한다.

Imitation Learning

사람(전문가)으로부터 observation $\bf o_t$와 action $\bf a_t$를 모아서 $\pi_\theta \bf (a_{t}|o_{t})$를 supervised learning 하는 것을 behavior cloning이라 한다.

검은선: training data의 trajectory 빨간선: 학습시킨 $\pi_{\theta}$의 trajectory

일반적으로 이러한 방법은 잘 안되는데 그 이유는 supervised learning이 정확하게 training data와 100% 똑같지 않기때문에 초반에 mistake가 일어나고 그 결과 모르는 trajectory로 가게 되고 계속해서 mistake가 커지기 때문이다.

문제 개선

End to End Learning for Self-Driving Cars 에서 위에서 나온 문제를 해결하기 위해 차에 3개의 카메라를 달아서 해결하였다. 왼쪽 카메라는 오른쪽 핸들로 bias를 오른쪽 카메라는 왼쪽 핸들로 bias를 주어 상호보완이 가능하게 하여 학습이 더 잘되게 하였다. 하지만 이 방법은 자율주행에서만 가능하다.

trajectory의 distribution 안정적이게 되었다.

$\bf p_{\text {data}}(o_t)$: training data(observation)의 distribution
$\bf p_{\pi_\theta}(o_t)$: $\pi_\theta$를 따랐을때 나온 observation 의 distribution

실제 training data는 $\bf p_{\text {data}}(o_t)$에서 sampling된 것으로 볼 수 있다.
여기서 $o_t$는 서로 독립적이지 않지만, supervised learning을 이용하기에 independent가 된다.

여기서 문제는 $\bf p_{\text {data}}(o_t)$와 $\bf p_{\pi_\theta}(o_t)$가 달라서 mistake가 생기게 된다는 것이다. 그렇다면 $\bf p_{\text {data}}(o_t) = p_{\pi_\theta}(o_t)$로 강제로 만들어 주면 어떻게 될까?

DAgger

여기서 우리는 policy를 data만큼 바꾸지 않을 것이다. DAgger의 idea는 training datg를 $\bf p_{\text {data}}(o_t)$가 아닌 $\bf p_{\pi_\theta}(o_t)$에서 모으는 것이다.

1. human data로 $\bf \pi_\theta (a_t|o_t)$를 학습 시킨다.
2. $\bf \pi_\theta (a_t|o_t)$로 새로운 데이터($o_t$)를 얻는다.
3. 사람이 새로운 데이터에 라벨($\bf a_t$)을 달아준다.
4. 새로 얻은 데이터를 training data에 합친다.
5. 1-4를 계속 반복한다.

하지만 사람이 label을 정의 해주기 힘들고 너무나 많은 노동력이 든다는 문제점이 생긴다.

만약 모델이 drift가 생기지 않을 정도로 학습이 잘되고 overfit 되지 않는다면 성능이 올라갈 것이다. 하지만 그렇게는 잘되지 않는다.

실패 원인

Non-Markovian behavior

$\bf \pi_\theta (a_t|o_t)$는 현재 observation에만 의존하여 행동하지만, 실제 사람은 과거의 observation도 고려하기에 문제가 발생하였다.

위 문제의 해결방안중 하나는 RNN이다.

Multimodal behavior

파란색 바그래프는 discrete case를 나타낸 것이고 밑에는 continuous 정규분포(Maximum Likelihood)로 나타낸 것이고 이는 적용되지않는다.

위 나무 그림처럼 같은 상황에서도 다양한 행동(왼쪽, 오른쪽)이 가능하다. 이러한 문제는 Output Mixture of Gaussians, Latent variable model, Autoregressive discretization으로 해결할 수 있다.

Output mixture of Gaussians

action을 선택할 때 한 개의 Gaussian에서 뽑는 것이 아닌 여려 개의 Gaussian을 이용하는 방법이다.
하지만 이 방법은 n개의 action만 사용 가능 하므로 action이 많을수록 사용하기 힘들다는 단점이 있다.

latent variable models

이 방법은 input에 노이즈를 추가해서 딥러닝 모델에 학습시킨다. 원하는 대로 표현이 가능하지만, 훈련이 어렵다는 단점이 있다.

autoregressive discretization

softmax를 통해 discrete한 확률분포를 뽑아내고 분포에서 sampling하여 또 다른 네트워크에 입력으로 넣어주고 다시 확률분포를 뽑아준다. 이 과정을 n번 반복하여 n개의 dimension을 출력으로 뽑아내게 된다.
이 방법은 만약 작은 차원의 action space를 가지고 있고 action space가 continuous이라도 discrete하게 바꿀 수 있다. 하지만 high dimential에서는 practical 하지 않다.

Imitation learning: recap

Behavior cloning은 종종 이 방법만으로 불충분하다. 왜냐하면, distribution mismatch problem이 발생하기 때문이다.

하지만 다음과 같은 방법을 쓰면 잘 작동한다.

1. Hacks (e.g 자율주행에서 카메라 3개를 쓴 방법)
2. 안정적인 trajectory distribution으로부터 sampling
3. on-policy data를 추가한다. (e.g Dagger 사용)
4. 더 정확하게 모델링 한다.

Imitation learning의 한계

• 사람이 data를 제공해야 한다.
  • 딥러닝은 data가 많을 때 잘된다.
• 사람이 특정 action을 정해주기 힘든 경우도 있다.
• 사람은 자동으로 배우는데 기계는 그렇지 못한다.
  • 스스로 경험으로부터 무제한 데이터가 필요
  • 연속적으로 스스로 improvement 해야 한다.

learning without imitation

$\delta$: 사자한테 먹히면 1 아니면 0

사자예시로 다시 돌아가보면 우리는 사자에게 먹히지 않는 것이 목표이다.(위 식의 기댓값을 minimize)

우리는 오늘도 내일도 모레도 먹히는 것을 원하지 않기에 위와 같이 state와 action의 sequence로 식을 바꿀 수 있다. 이 식은 강화학습 문제와 비슷하게 된다.

• cost function: 얼마나 나쁜 결과를 했는지를 나타낸다.(minimize)
• reward function: 얼마나 잘했는지를 나타낸다(maximize)

cost function for imitation learning

imitation learning에서 reward function은 $\bf r(s,a) = \log p(\bf a = \pi ^\star (s)|s)$($\bf p(\bf a = \pi ^\star (s)|s)$은 action과 optimal policy가 같을 확률)으로 나타내고 cost function은 위 식과 같이 $\bf c(s,a)$로 나타내고 이는 틀린 횟수로 볼 수 있다.

Distribution mismatch analysis

distribution mismatch 문제에서 time 축을 time step $\bf T$로 정의하고, cost function을 $\bf r(s,a) = \log p(a=\pi^\star (s) | s)$로 log likelyhood loss를 사용해도 되지만 간단하게 분석하기 위해서 zero-one loss를 사용한다.

$$\bf c(s,a) = \begin{cases}
0 & \ \ \text{ if } \ a = \pi ^\star (s) \ \cr
1 & \ \ \ \text{otherwise.}
\end{cases} - (8) $$

tightrope로 예시를 들면, 위 grid 그림처럼 나타낼 수 있다.(빨간색이 낭떠러지)

학습이 어느정도 되서 모든$\bf s \in \mathit{D_{train}}$에 대해 $\pi_{\theta}(a \ne \pi^\star (s) | s) \leq \epsilon$이라 가정하자. 학습데이터의 모든 state에서 사람과 다른 행동(줄에서 떨어짐)을 할 확률이 $\epsilon$ 보다 작다는 것을 말한다($\epsilon$을 mistake할 확률으로 볼 수 있고 worst case이다.). $\epsilon$은 training method에 따라 값이 달라지고 method가 좋을수록 값이 작아진다.

이때 total cost 기댓값의 upper bound는 다음과 같다.

$$\bf \mathbb{E} \left[\ \mathsf{\underset{t}{\sum}}\ c(s_{t},a_{t})\right] \leq \epsilon T + (1-\epsilon)(\epsilon(T-1) + (1-\epsilon)(…))$$

첫번째 step에서 mistake했을때 cost의 기댓값은 $\bf \epsilon \bf T$(mistake를 하면 그 이후 step에서는 계속 mistake하므로)이고 첫번째는 잘하고 두번째 step에서 mistake했을때 cost의 기댓값은 $\bf (1-\epsilon)\epsilon(T-1)$이고 $\bf T$ step만큼의 항이 나온다. 그리고 각가의 항이 $\bf O(\epsilon T)$(Order of T)이기 때문에 $\bf \mathbb{E} [\ \mathsf{\underset{t}{\Sigma}}\ c(s_{t},a_{t})]$의 bound는 $O(\epsilon T^2)$가 된다.

하지만 $O(\epsilon T^2)$는 좋지 않다. 왜냐하면 $\epsilon$이 아무리 작아도 $T$가 길어질수록 cost가 커지기 때문이다.

위에서 했던 가정 “모든 $\bf s \in \mathit{D_{train}}$”은 trained state만 고려하기에 적절한 가정은아니다(image classification에서 train과 test를 똑같은 사진을 쓰는 것과 같음, generalization 문제). 그래서 가정을 $\bf s \sim p_{train}(s)$으로 바꾸자.

먼저 DAgger를 적용했을 때 $p_{train}(s) \rightarrow p_\theta(s)$($p_{train}(s) = p_\theta(s)$)이 된다. 이때 total cost 기댓값의 upper bound는

$$\bf \mathbb{E} \left[\ \mathsf{\underset{t}{\sum}}\ c(s_{t},a_{t})\right] \leq \epsilon T$$
이된다.(매 step마다 mistake할 확률이 $\epsilon$으로 동일하기 때문)

이제 DAgger를 쓰지않고 $\bf p_{train}(s) \ne p_{\theta}(s)$(train data의 상태분포와 trained된 상태분포가 다름)라 가정하자.

$$ \bf p_{\theta}(s_{t}) = (1-\epsilon)^t p_{train}(s_{t}) + (1-(1-\epsilon)^t)p_{mistake}(s_t)$$

여기서 $(1-\epsilon)^t$는 mistake를 하지 않을 확률이고 $\bf p_{mistake}(s_{t})$는 mistake했을때 확률분포이다.

$$ \bf | p_{\theta}(s_{t}) - p_{train}(s_{t})| = \underset{s_{t}}{\sum} | p_{\theta}(s_{t}) -p_{train}(s_{t}) $$

total variation divergence between $p_\theta(s_t)$ and $p_{train}(s_t)$

$$\bf p_{\theta}(s_{t}) = (1-\epsilon)^t p_{train}(s_{t}) + (1-(1-\epsilon)^t)p_{mistake}(s_t)$$

$$\bf p_{train}(s_t) = (1-\epsilon)^t p_{train} + (1-(1-\epsilon)^t)p_{train}$$

이므로

$\bf \left| p_{\theta}(s_{t}) - p_{train}(s_{t}) \right| = (1-(1-\epsilon)^t) \left| p_{mistake}(s_{t})-p_{train}(s_{t}) \right|$이된다.

$$\bf \left| p_{\theta}(s_{t}) - p_{train}(s_{t}) \right| = (1-(1-\epsilon)^t) \left| p_{mistake}(s_{t})-p_{train}(s_{t}) \right| \leq 2(1-(1-\epsilon)^t) \leq 2\epsilon t$$

두 확률분포의 차이의 절댓값($\bf \left| p_{mistake}(s_{t})-p_{train}(s_{t}) \right|$)의 최댓값은 2이고 $\bf -(1-\epsilon)^t \leq -(1-\epsilon t)$ for $\epsilon \in \left[0,1\right]$이므로 $\bf \left| p_{mistake}(s_{t})-p_{train}(s_{t}) \right|$의 upper bound는 $2\epsilon t$이 된다.

cost의 기댓값은 아래와 같이 전개된다.

$$\bf \underset{t}{\sum} \mathbb{E_{p_{\theta}(s_{t})}} \left[ c_{t} \right] = \underset{t}{\sum}\underset{s_{t}}{\sum} p_{\theta}(s_{t})c_{t}(s_{t})$$

$$\bf p_\theta c = p_{train}c + (p_\theta - p_{train})c \ \ \ \because \bf p_\theta = p_{train} + p_\theta - p_{train}$$

$$\bf \leq p_{train}c + |p_\theta-p_{train}|c \leq p_{train}c + |p_\theta-p_{train}|c_{max}$$

$$\bf p_\theta = p_{train} + p_\theta - p_{train}$$

$$\bf \underset{t}{\sum} \mathbb{E_{p_{\theta}(s_{t})}} \left[ c_{t} \right] = \underset{t}{\sum}\underset{s_{t}}{\sum} p_{\theta}(s_{t})c_{t}(s_{t}) \leq \underset{t}{\sum}\underset{s_{t}}{\sum} p_{train}(s_{t})c_{t}(s_{t}) + \left| p_{\theta}(s_{t}) -p_{train}(s_{t})\right|c_{max}$$

여기서 $\bf c_{max}$(worst possible cost)는 cost definition에 의해 1이고 $p_{train}$의 cost 기댓값 $\bf \underset{s_{t}}{\sum}p_{train} (s_{t})c_{t}(s_{t})$은 $\epsilon$이기때문에 아래와 같이 전개된다.

$$\bf \underset{t}{\sum} \mathbb{E_{p_{\theta}(s_{t})}} \left[ c_{t} \right] \leq \underset{t}{\sum}\epsilon + 2 \epsilon t \leq \epsilon T + 2 \epsilon T^{2}$$

결국 $\bf O(\epsilon T^{2})$이 된다.