PRML 1 Introduction

작성일 Edited on In 댓글:

0.Introduction

패턴인식(Pattern Recognition) & 머신러닝(Machine Learning)

  • Pattern Recognition이란 computer 알고리즘을 사용하여 데이터에 내재된 패턴을 자동으로 찾는 것을 의미한다.

  • 아래와 그림과 같이 필기체를 분류(classification)하는 문제가 있다고 하자

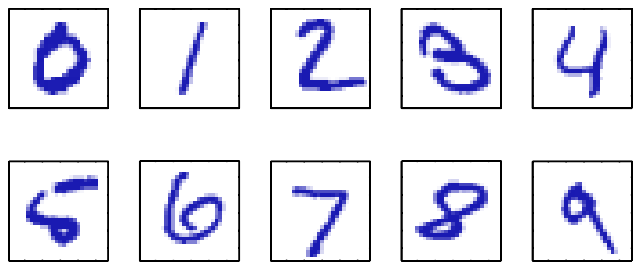
$\bf x$:숫자의 이미지 $\bf y$: 숫자의 class

  • 다음과 같은 문제는 Rule-based(heuristics)한 방법으로 해결할 수 있지만 실제로 이러한 방법은 예외사항을 계속해서 만들어야 하므로 안 좋은 결과를 만들게 된다.

  • 더 좋은 방법은 training set을 사용하여 model의 parameters를 조절하는 machine learning을 사용하는 것이다.

  • machine learning의 결과는 $\bf x$를 input으로 받고 output으로 $\bf y$를 내보내는 $y({\bf x})$로 표현할 수 있다.

  • 이 함수는 training data를 기반으로 training(learing)을 거치며 원하는 함수에 가까워 진다.

  • training된 모델로 test set 이라 부르는 새로운 데이터의 결과를 알 수 있습니다.

일반화(Generalization)

  • training 동안 사용되지 않은 data를 올바르게 분류하는 능력을 generalization이라 한다.

  • generalization은 pattern recognition의 주된 목적이다.

전처리(Pre-Process)

  • 대부분의 상황에서 입력데이터를 문제를 더 쉽게 해결하기 위해서 전처리(pre-process)라 한다.

  • 이러한 전처리과정은 test data도 train data에서 한 것과 똑같이 적용해야 한다.

  • 전처리 과정은 data의 목적은 연산 속도를 높이고 데이터를 더 쉽게 다루기 위해서 이다.

    • 전처리 과정에서 정보를 잃게되는데 그로인해 전체적인 성능이 저하되지 않도록 조심해야한다.

Machine Learning의 종류

지도학습(Supervised Learning) Problem

input vectors와 상응하는 target vectors가 있는 문제

  • 분류(classification)

    • target vectors가 유한개의 discrete categories인 문제
      • 예) 필기체 숫자 분류

  • 회귀(regression)

    • target vectors가 continuous 변수인 문제
      • 예) 주식 가격 예측

비지도학습(Unsupervised Learning) Problem

target vectors없이 input vectors만 존재하는 문제

  • 클러스터링(clustering)

    • 데이터내에서 비슷한 속성을 가지는 그룹을 찾는 문제

  • 밀도 추청(density estimation)

    • 입력 데이터로 변수의 분포를 도출하는 문제 (변수 $\neq$ 입력데이터)

  • 시각화(visualization)

    • 고차원 공간의 데이터를 2 또는 3 차원 공간에 투영하는 보여주는 것

강화학습(reinforcement learning)

주어진 상황에서 reward를 최대화 하기위한 적절한 actions를 찾는 문제

  • 강화학습은 지도학습처럼 optimal한 outputs이 주어지지 않고 trial and error를 통해서 학습한다.

  • 대부분의 경우, 현재의 action은 즉각적인 reward 뿐만 아니라 이후의 reward에도 영향을 끼칩니다.

  • 어떤 action은 좋은 결과를 어떤 action은 덜 좋은 결과를 불러오는데 이러한 것을 정확히 알지 못하는 문제를 신뢰 활당 문제(credit assignment problem)이라 한다.

  • 강화학습의 특징 중 하나는 탐색(exploration, 효율적인 새로운 행동을 찾는 것)과 활용(exploitation, 높은 보상을 주는 쪽으로 행동하는 것)의 trade-off 문제를 해결하는 것이다.

  • 이 책에서는 다루지 않는다.

1. Example: Polynomial Curve Fitting

Polynomial Curve Fitting

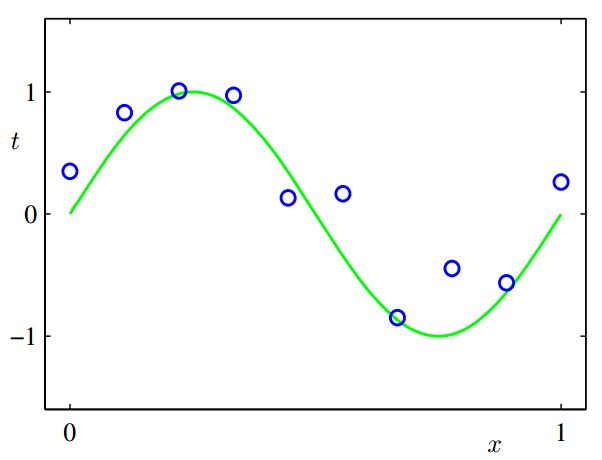
0과 1사이에서 10개의 샘플을 뽑아 입력 변수를 $x$라고 하자. 초록색 선은 $\sin (2\pi x)$ 이다. 우리의 목표는 새로운 입렵 변수의 타겟 값 $t$를 올바르게 예측하는 것이다.

  • 위 그림에서 주어진 데이터들은 랜덤하게 noise가 더해져 있다.(푸른색 동그라미가 초록색선위에 있지 않다.)

  • 이 문제를 간단한 curve fitting 방식으로 접근해보자

$$ y(x,{\bf w})=w_0+w_1x+w_2x^2+…+w_Mx^M=\sum_{j=0}^{M}w_jx^{j} \qquad{(1.1)} $$

  • $M$: 다항식의 차수

  • $y(x,{\bf w})$가 $x$에 대하여 비선형이지만 계수 ${\bf w}$에 대해서는 선형 함수이다.

  • 다항 함수와 같이 알려지지 않는 변수 ${\bf w}$에 대해 선형인 함수를 선형 모델(linear models)라 불린다. (Chapters 3와 4에 자세히 다룸)

error function

  • 계수 ${\bf w}$는 training data를 통해 다항 함수를 fitting함으로써 결정된다.

  • 이러한 방법은 error function(함수 $y(x,{\bf w})$와 target 변수$t$의 차이)를 최소화 함으로써 가능하다.

  • 간단한 error function의 예로 오차의 제곱합이 있다.

$$ E({\bf w})=\dfrac{1}{2}\sum_{n=1}^{N}{y(x_n,{\bf w})-t_n}^2 \qquad{(1.2)} $$

$\frac{1}{2}$는 계산의 편의를 위해서 사용됨

  • 주어진 error function이 이차형식(quadratic)의 함수 꼴이므로 최소화 하는 값은 유일 해를 가지게 됨을 보장 받는다.

  • 결과적으로 얻어지는 함수 값은 $y(x, {\bf w}^*)$이다.

    • ${\bf w}^*$는 유일 해를 가질때 ${\bf w}$이다.

Model Comparison(Model Selection)

  • 다항식의 차수 $M$를 고르는 문제가 있는데 이를 model comparison 또는 model selection이라 한다.

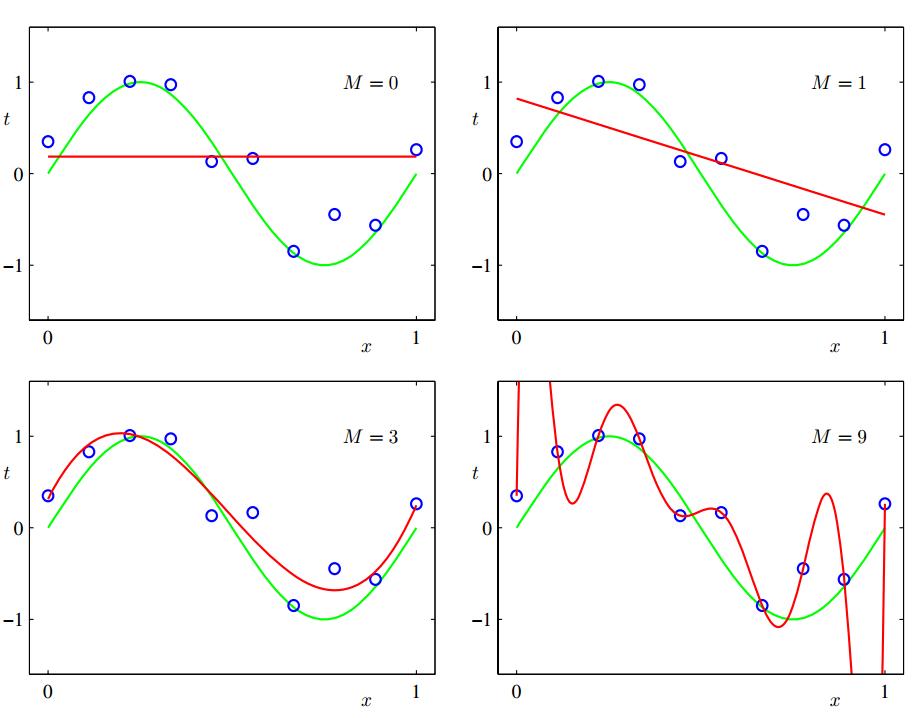
  • $M=0$,$M=1$일때 training data와 목표인 $\sin (2\pi x)$모두 fit하지 않는데 이런 경우를 under-fitting이라 한다.

  • $M = 9$일때 training data와 가장 잘 fit하지만 $\sin (2\pi x)$와는 fit 하지 않는 것을 확인할 수 있다. 이런 경우를 over-fitting이라 한다.

  • 우리의 목표는 새로운 데이터에 대해서 정확한 예측하는 좋은 일반화(generalization) 모델을 찾는 것이다.