7.1 행렬, 벡터: 합과 스칼라곱
행렬(matrix)
- 수(혹은 함수)를 직사각형 모양으로 괄호 안에 배열한 것(사각행렬)
- 원소(Entry) 또는 요소(Element): 행렬에 배열되는 수(혹은 함수)
- 행(Row) : 수평선
- 열(Column) : 수직선
일반적인 표기법과 개념
$$ {\bf A} = [a_{jk}] =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
a_{21} & a_{22} & \cdots & a_{2n} \cr
\vdots & \vdots & \ddots & \vdots \cr
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix} : m \times n 행렬 $$
- 행렬은 볼드체의 대문자를 사용한다.
- 첫 번째 아래 첨자 $j$는 행(Row)
- 두 번째 아래 첨자 $k$는 열(Column)
- $a_{jk}$: $j$ 행, $k$ 열의 원소(Element)
- $m \times n$은 행렬의 크기(size)를 나태는 것이다.
정방행렬(square matrix)
- $m=n$ 이라면 A는 정사각형 모양이다
- 정방행렬에서 원소 $a_{11}, a_{22}, \cdots , a_{nn}$을 포함하는 대각선을 행렬 $A$ 의 주대각선(Principal Diagonal)이라고 한다
$ {\bf A} = [a_{jk}] =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
a_{21} & a_{22} & \cdots & a_{2n} \cr
\cdot & \cdot & \cdots & \cdot \cr
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}$
계수행렬(coefficient matrix)
- 선형연립방정식의 계수 만으로 이루어진 행렬
*통상, 선형 연립방정식을 $\bf Ax = b$ 로 나타낼 때, 행렬 A를 말한다.
ex) $ \bf \widetilde A =
\begin{bmatrix}
4 & 6 & 9 \cr
6 & 0 & -2 \cr
5 & -8 & 1
\end{bmatrix}$
첨가행렬(augmented matrix)
- 계수행렬 및 우변 상수항을 모두 포함한 행렬
- 계수행렬 및 우변 상수항을 모두 포함한 행렬
- 각 행이 선형연립방정식의 하나의 식과 대응되는 행렬
ex) $ \bf \widetilde A =
\begin{bmatrix}
4 & 6 & 9 & 6 \cr
6 & 0 & -2 & 20 \cr
5 & -8 & 1 & 10
\end{bmatrix}$
벡터(Vector)
- 단 하나의 행, 또는 하나의 열만으로 이루어진 행렬
- 벡터의 성분을 성분(component)라 한다.
- 벡터는 소문자 볼드체 문자 $\bf a, b, c,\cdots,$ 또는 $\bf a = [a_j]$로 표현한다.
행벡터(Row Vector)
하나의 행으로 구성된 행렬
$$ {\bf a} = \begin{bmatrix} a_1, a_2, \cdots, a_n \end{bmatrix}$$
열벡터(Column Vector)
하나의 열로 구성된 행렬
$$ {\bf b} = \begin{bmatrix} b_1\cr b_2\cr \vdots \cr b_n \end{bmatrix} $$
행렬의 상등(Equality of Matrices)
두 행렬 A와 B의 크기가 같고 대응하는 성분들이 모두 같을 경우 ($A = B$)
행렬의 합(Matrix Addition)
같은 크기의 행렬에 대해서만 정의되고 그 합은 대응하는 원소를 각각 합함으로 얻어진다.
스칼라곱(Scalar Multiplication)
행렬의 각 원소에 상수(Scalar)를 곱(Product)하여 얻어진다.
행렬의 가법과 스칼라곱에 대한 연산법칙
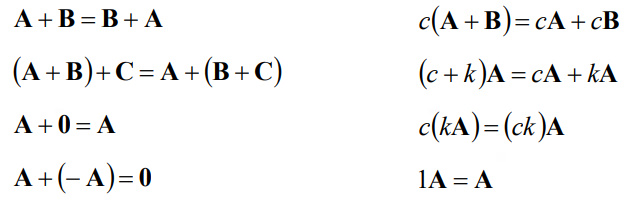
7.2 행렬의 곱
행렬과 행렬의 곲(Matrix Multiplication)
$r \times p$행렬 $B = [b_{jk}]$의 행수 $r$와 $m \times n$행렬 $A = [a_{jk}]$의 열수 $n$가 서로 같아야 정의되며 $$c_{jk} = \sum_{j=1}^n a_{jl}b_{lk} = a_{j1}b_{1k} +a_{j2}b_{2k} + \cdots + a_{jn}b_{nk}$$
를 원소로하는 $m\times p$ 행렬로 정의된다.($AB$는 정의되지만 BA는 정의되지 않을 수 있다.)
- 행렬의 곱은 비가환적(Not Commutative)이다. 즉 $AB \neq BA$
행렬의 곱에 대한 연산 법칙
$$ (kA)B = k(AB) = A(kB)$$
$$ A(BC) = (AB)C\ \ \ \ \ \text{(결합법칙(Associative Law))}$$
$$ (A+B)C = AC + BC\ \ \text{(분배법칙(Distrivutive Law))}$$
$$ C(A+B) = CA + CB\ \ \text{(분배법칙(Distrivutive Law)} $$
행렬과 벡터의 전치(Transposition of Matrices)
열과 행이 서로 바뀌어 얻어진 행렬
$$ {\bf A^T} = [a_{kj}] =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{m1} \cr
a_{21} & a_{22} & \cdots & a_{m2} \cr
\vdots & \vdots & \ddots & \vdots \cr
a_{1n} & a_{2n} & \cdots & a_{mn}
\end{bmatrix}$$
- 정방행렬에 대한 전치는 주대각선에 관하여 대칭으로 위치된 원소들을 서로 바꾼 것이다.
전치 연산에 대한 법칙
$$ (A^T)^T =A $$
$$ (A + B)^T = A^T +B^T $$
$$ (cA)^T = cA^T $$
$$ (AB)^T = B^TA^T $$
특수한 행렬(Special Matrices)
대칭행렬(Symmetric Matrix)
전치가 본래의 행렬과 같은 정방행렬 ($A^T = A$)
반대칭행렬(Skew- symmetric Matrix)
전치가 본래의 행렬의 음이 되는 정방행렬 ($A^T = -A$)
삼각행렬(Triangular Matrix)
- 위삼각행렬(Upper Triangular Matrix)
- 주대각선을 포함하여 그 위쪽으로만 0이 아닌 원소를 갖는 정방행렬
- 아래삼각행렬(Lower Triangular Matrix)
- 주대각선을 포함하여 그 아래쪽으로만 0이 아닌 원소를 갖는 정방행렬
대각행렬(Diagonal Matrix)
주대각선 상에서만 0이 아닌 원소를 가질 수 있는 정방행렬
스칼라 행렬(Scalar Matrix)
주대각선 원소들이 모두 같은 대각행렬
단위행렬(Unit 또는 Identity Matrix)
주대각선 원소들이 모두 1은 대각행렬
7.3 선형연립방정식, Gauss 소거법
선형연립방정식(=선형계(linear systems))
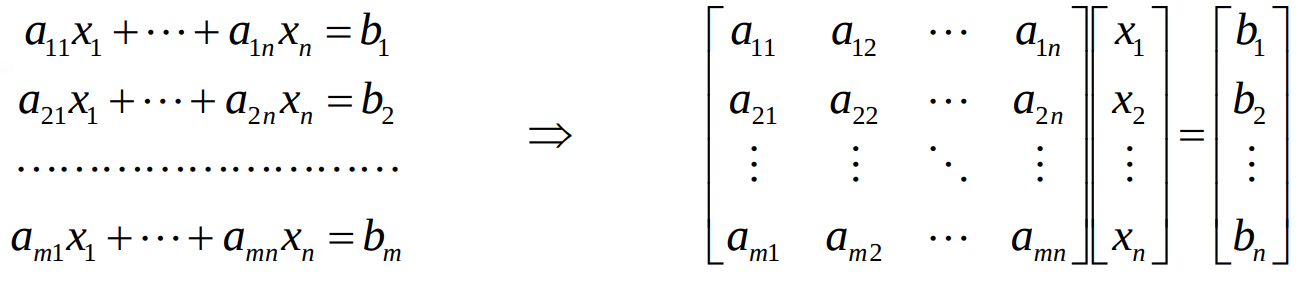
- 제차연립방정식(Homogeneous Simultaneous System)
- $b_j$가 모두 0인 경우
- 비제차연립방정식(Nonhomogeneous Simultaneous System)
- $b_j$중 적어도 하나는 0이 아닌 경우
선형연립방정식의 행렬표현 : $\bf Ax = b$

- 계수행렬(Coefficient Matrix) : $\bf A$
- 해벡터(Solution Vector) :$\bf x$
- 첨가행렬(Augmented matrix) : 계수행렬 $\bf A$에 열벡터 $\bf b$를 첨가한 행렬
가우스 소거법과 후치환(Gauss Elimination and Back Substitution)

- $x_1$을 소거 : 첫 번째 식에 두 배 한 후, 이를 두 번째 식에 더한다.

후치환(Back Substitution) :$x_2, x_1$ 순으로 해를 구한다.
마지막 방정식에서 해를 구한 후, 그 결과를 역순으로 첫째 방정식에 대입하여 정리한다.

기본행연산. 행동치 연립방정식(Elementary Row Operations. Row-Equivalent Systems)
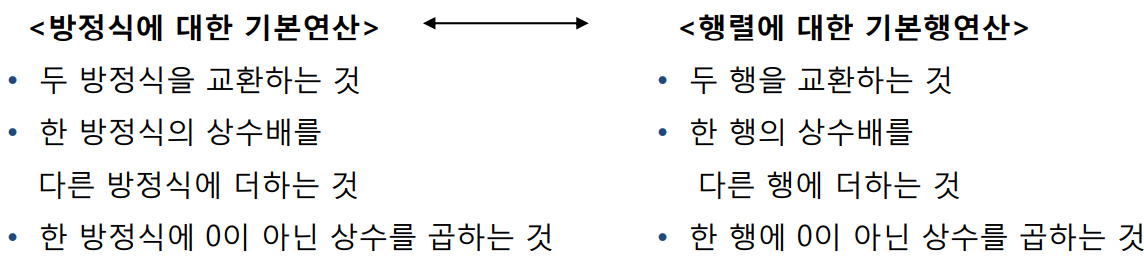
기본 행연산을 이용하여 미지수를 하나씩 소거하여 대각선 아래의 계수를 0으로 만든다
행동치(Row-Equivalent)
선형시스템 $S_1$이 선형시스템 $S_2$에 유한번의 기본행연산을 가하여 얻어질 수 있다면 $S_1$을 $S_2$의 행돋치라 한다.
행동치 연립방정식(Row-Equivalent Systems)
- 행동치 연립방정식들은 같은 해집합을 갖는다.
- 지금까지 행연산에 국하여 다루었고 열연산의 경우 해집합에 영향을 미칠 수 있다.
- 미지수보다 더 많은 방정식을 가진다면 과잉한정(overdetermined)
- 미지수보다 적은 방정식을 가지면 과소한정(underdetermined)
행사다리꼴(Row Echelon Form)과 행 사다리꼴로부터의 정보
행사다리꼴
Gauss 소거법의 마지막 단계에서 보는 계수행렬과 첨가행렬의 형태와 이에 대응하는 연립방정식
각 행에서 가장 왼편에 있는 0아닌 성분을 모두 1로 만든 것을 축소된 사다리꼴(reduced echelon form)이라 한다.

- 3가지 가능한 경우
- 정확하게 하나의 해가 존재한다. : $r=n$이고 $\widetilde{b_{r+1}}, \cdots, \widetilde{b_m}$이 모두 0이다.
- 무한히 많은 해가 존재한다. : $r < n$이고 $\widetilde{b_{r+1}}, \cdots, \widetilde{b_m}$이 모두 0이다.
- 해가 없다. : $r < m$이고 $\widetilde{b_{r+1}}, \cdots, \widetilde{b_m}$중 하나라도 0이 아니다.(모순이 없는 경우, $r = m$이거나$, $r < m$이더라도 $\widetilde{b_{r+1}}, \cdots, \widetilde{b_m}$가 모두 0이라면 해가 존재한다.)
7.4 일차 독립. 행렬의 계수. 벡터공간
벡터의 일차 독립과 종속성

- 일차 독립(Linearly Independent) : 모든 $c_j = 0$ 일 때만 위 식이 만족
- 일차 종속(Linearly Dependent) : 어떤 $c_j \neq 0$ 이어도 위 식이 만족
행렬의 계수(Rank)
행렬에서 1차독립인 행벡터의 최대수이며 rank($\bf A$)라 표시
행동치인 행렬
행동치인 행렬들은 같은 계수를 갖는다.
일차종속성과 일차독립성
각각 $\bf n$개의 성분을 갖는 $\bf p$개의 벡터들은 이 벡터들을 행벡터로 취하여 구성된 행렬의 계수가 $\bf p$이면 일차독립이고, 그 계수가 $\bf p$보다 작으면 일차종속이다.
열벡터에 의한 계수
행렬의 계수는 행렬의 일차독립인 열벡터의 최대수와 같다.
=> 행렬과 행렬의 전치는 같은 계수를 갖는다
벡터의 일차종속
$\bf n$개의 성분을 갖는 벡터가 $\bf p$개 있고 $\bf n < p$ 라면 이들 벡터들은 항상 일차종속이다.
벡터공간 (Vector Space)
공집합이 아닌 벡터의 집합에 속해 있는 임의의 두 원소에 대하여, 이들의 일차결합이 다시 집합의 원소가 되며 다음 법칙을 만족하는 벡터들의 집합
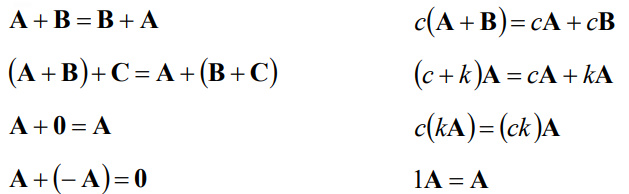
차원(Dimension)
벡터공간내의 일차독립인 벡터들의 최대수이며 $\bf \dim(V)$로 표기
기저(Basis)
벡터공간내의 최대로 가능한 수의 일차독립인 벡터로 구성되는 부분집합이며 기저가 되는 벡터의 수는 차원과 같다.
생성공간(Span)
성분의 수가 같은 벡터들에 관한 일차결합으로 표환되는 모든 벡터들의 집합
부분공간(Subspace
벡터공간에서 정의된 벡터합과 스칼라곱에 관하여 닫혀있는 부분집합
$\bf R^n$ 벡터공간
$\bf n$개의 성분을 갖는 모든 벡터들로 이루어진 벡터공간 $\bf R^n$의 차원 $n$이다.
행공간(Row Space)
행벡터들의 생성공간
열공간(Column Space)
열벡터들의 생성공간
행공간과 열공간
행렬의 행공간과 열공간은 차원이 같고, 행렬의 계수와도 동일하다.
영공간(Null Space)
$\bf Ax = 0$의 해집합
퇴화차수(Nullity)
영공간의 차원
$\bf A$의 계수 + $\bf A$의 퇴화차수 = 행렬 $\bf A$의 행 갯수
7.5 선형연립방정식의 해 : 존재성, 유일성
선형연립방정식에 대한 기본정리
존재성(Existence)
선형연립방정식이 모순이 없기 위한(Consistent), 다시 말해서 해를 갖기 위한, 필요충분조건은 계수행렬과 첨가행렬이 같은 계수를 갖는 것이다.
유일성(Uniqueness)
선형연립방정식이 유일한 해를 갖기 위한 필요충분조건은 계수행렬과 첨가행렬이 같은 계수를 갖는 것이다
무수히 많은 해(Infinitely Many Solutions)
계수행렬과 첨가행렬이 같은 계수$\bf r$을 갖고 $\bf r < n$이면, 무수히 많은 해가 존재한다.
Gauss 소거법(Gauss Elimination)
해가 존재하면 Gauss 소거법에 의해 모두 구해질 수 있다.
제차연립방정식
- 제차연립방정식은 항상 자명한 해(Trivial Solution)을 갖는다.
- 자명하지 않은 해가 존재할 필요충분조건 : $\bf r < n$ (계수행렬의 계수= $\bf r = \text{rank} A$, 미지수의 갯수 = $ \bf n$)
- $\bf r < n$이면 해공간은 $\bf n-r$차원 벡터공간이다.
- 제차연립방정식의 두 해벡터의 일차결합도 제차연립방정식의 해이다.
미지수보다 방정식의 수가 적은 제차 선형연립방정식
방정식의 수가 미지수의 수보다 적은 제차연립방정식은 항상 자명하지 않은 해(Nontrivial Solution)를 갖는다.
비제차연립방정식
만약 비제차 연립방정식이 해를 갖는다면 모든 해는
$$\bf x = x_0 + x_h$$
와 같은 형태가 된다.
$\bf x_0$은 고정된 임의의 해이고 $\bf x_h$는 대응하는 제차연립방정식의 모든 해를 대표한다.
7.6 참고사항 : 2차 및 3차 행렬식
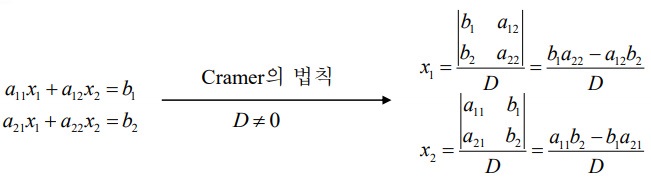
2차 행렬식(Determinant of Second Order)

선형연립방정식
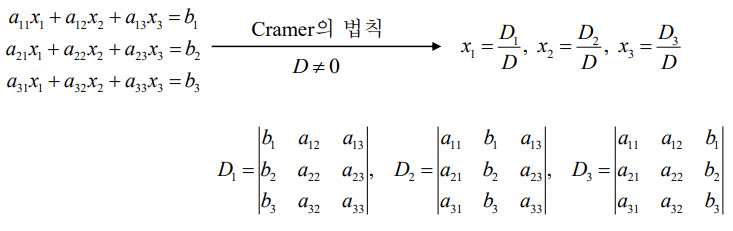
3차 행렬식(Determinant of Third Order)

선형연립방정식
7.7 행렬식. Cramer의 법칙
$\bf n$차 행렬식(Determinant of Third Order)
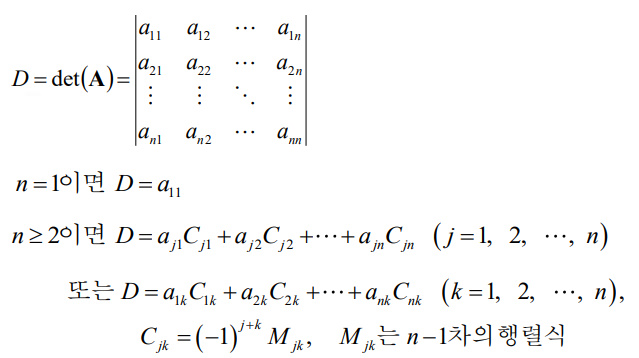
- 소행렬식(Minor): $M_{jk}$
- 여인수(Cofactor): $C_{jk}$
기본행연산항(Elementary Row Operation)에서의 $\bf n$차 행렬식의 변화
- (a) 두 행을 바꾸는 것은 행렬식의 값에 -1을 곱하는 것이다
- (b) 한 행의 상수배를 다른 행에 더하는 것은 행렬식의 값에 변화를 주지 않는다.
- (c) 한 행에 0이 아닌 $c$를 곱하면 행렬식의 값이 $c$배가 된다.
$\bf n$차 행렬식의 추가적인 성질
- (a)-(c)는 열에 대해서도 성립한다.
- (d) 전치(Transposition)는 행렬식의 값에 변화를 주지 않는다.
- (e) 0행 또는 0열은 행렬식의 값을 0으로 만든다.
- (f) 두 행이나 두 열이 비례관계에 있으면 행렬식의 값은 0이다. 특히 같은 두 행이나 두 열을 가진 행렬식의 값은 0이다.
행렬식과 계수
$m \times n$ 행렬 $A=[a_{jk}]$가 계수 $r(\geq 1)$을 갖기 위한 필요충분조건은
(1) $\bf A$가, 0이 아닌 행렬식을 갖는 $r \times r$ 부분행렬을 가지고,
(2) $\bf A$의 $(r+1) \times (r+1)$ 또는 그보다 큰 크기의 모든 정방 부분행렬(그런 부분행렬이 존재할 경우)의 행렬식이 0이 되는 것이다.
특히, $\bf A$가 정방행렬 $ n \times n$ 정방행렬일 때, 계수가 $n$일 필요충분조건은
(3) $\text{det}A \neq 0$이다.
Cramer의 정리(행렬식에 의한 선형연립방정식의 해)

$D \neq 0이면 그 연립방정식은 오직 하나의 해를 갖는다.
- $D_k$는 $D$의 $k$번째열을 $b_1, \cdots, b_n$을 성분으로 하는 열벡터로 대치하여 얻은 행렬식이다.
- 따라서 위 식이 제차이고 $D \neq 0$이면, 그것은 오직 자명한 해 $x_1 = 0, x_2 = 0, \cdots, x_n = 0$만을 갖는다.
- 만약 $D = 0$이면, 제차연립방정식은 자명한 해가 아닌 해도 갖는다.
7.8 역행렬. Gauss-Jordan 소거법
역행렬(Inverse Matrix)

- 정칙행렬(Nonsingular Matrix) : 역행렬을 갖는 경우
- 특이행렬(Singular Matrix) : 역행렬을 갖지 않는 경우
- 역행렬을 가지면 그 역행렬은 유일하다
역행렬의 존재성
$\bf A$가 $\bf n \times n$행렬일 때, 역행렬$A^{-1}$이 존재할 필요 충분조건은 $\text{rank}A = n$이다.($\bf \text{det}A \neq 0$도 같은 조건이다)

Gauss-Jordan 소거법에 의한 역행렬의 결정

행렬식에 의한 역행렬 공식

여인수 $C_{jk}$가 놓인 위치는, 행렬 $\bf A$의 성분 $a_{jk}$가 놓인 자리가 아니라, 성분 $a_{kj}$가 있는 자리이다.
대각행렬의 역행렬
대각행렬 ${\bf A} =[a_{jk}](즉, $j \neq k$일 때 $a_{jk} = 0$)가 역행렬을 가질 필요충분조건은 주대각선 상의 모든 성분 $a_{jj}$가 0이 아니어야 한다.
$$ 이 경우 \bf A^{-1}은 \frac 1 a_{11}, \cdots, \frac 1 a_{nn}들이 대각원소인 대각행렬이 된다.$$

두 행렬의 곱 $\bf AC$의 역행렬
$$\bf(AC)^{-1} = C^{-1}A^{-1}$$
$$\bf (AC\cdotsPQ)^{-1} = Q^{-1}P^{-1}\cdots C^{-1}A^{-1}$$
역행렬의 역행렬
$$\bf (A^{-1})^{-1} = A$$
행렬의 곱에 대한 특이 성질, 소거법
- 행렬의 곱은 교환법칙이 성립하지 않는다.(일반적으로 성립하지 않는다.)
$$ \bf AB \neq BA$$
- $\bf AB = 0$일 때 $\bf A = 0$ 또는 $\bf B = 0$이 아닐 수도 있다.
$$\begin{bmatrix}
1 & 1 \cr
2 & 2
\end{bmatrix}
\begin{bmatrix}
-1 & 1 \cr
1 & -1
\end{bmatrix} =
\begin{bmatrix}
0 & 0 \cr
0 & 0
\end{bmatrix}
$$
- $\bf AC = AD$일 떄 $C \neq D$일 수도 있다.(심지어 $A \neq 0$ 일 때에도))
소거법칙
- $\bf A,B,C$를 $n \times n$ 행렬이라 하자.
- (a) $\text{rank} A = n$이고 $\bf AB = AC$이면, $B = C$이다.
- (b) $\text{rank} A = n$이면 $\bf AB = 0$은 $\bf B = 0$을 의미한다.
- 그러므로 $\bf AB = 0$이면서 $\bf A \neq 0$이고 동시에 $\bf B \neq 0$이면, $\text{rank} {\bf A} < n$이고 $\text{rank} {\bf B} < n$이다.
- $\bf A$가 특이행렬이면, $\bf BA$와 $\bf AB$도 특이행렬이다.
행렬곱의 행렬식
$\bf \det (AB) = \det (BA) = \det A \det B
7.9 벡터공간, 내적공간, 일차변환
실벡터공간(Real Vector Space)
성분 $\bf a,b,\cdots$을 갖는 공집합이 아닌 집합 $V$에 대하여 “벡터의 덧셈”과 “스칼라 곱”이라고 하는 두 가지 대수학적 연산법칙이 다음과 같이 정의되어 있으면, 이 집합 $V$를
실벡터공간(real vector space, 또는 실선형 공간(real linear space))이라 부르고 $V$의 성분을벡터라 부른다.
벡터의 덧셈: $\bf a + b$
- 가환성(Commutativity) $\bf a+b = b+a$
- 결합성(Associativity) $\bf (u+v) + w = u + (v+w)$
- 영벡터(Zero Vector) $\bf a+0=a, a+(-a)=0$
스칼라곱: $k{\bf a}$
- 분배성(Distributivity) $c({\bf a+b}) = c{\bf a} + c{\bf b}$
- 분배성(Distributivity) $(c+k){\bf a} = c{\bf a} + k{\bf a}$
- 결합성(Associativity) $c(k{\bf a}) = (ck){\bf a}, 1{\bf a} = {\bf a}$
실내적공간(Real Inner Product Space)
실벡터공간 $V$에 속한 임의의 한 쌍의 벡터 $\bf a,b$에 대하여 하나의 실수를 대응시키는 규칙이 존재하여 다음 공리를 만족한다면, $V$를
실내적공간(real inner product space)이라 부른다.
내적(Inner Product)
$$ (a,b) = a \cdot b $$
- 선형선 $q_1{\bf a} + q_2{\bf b,c} = q_1({\bf a,c}) + q_2({\bf b,c})$
- 대칭성 $\bf (a,b) = (b,a)$
- 양의정치성(Positive-definiteness)
$\begin{cases}
(a,a) \geq 0, \cr
(a,a) = 0 \text{일 필요충분조건은} \ \ a = 0
\end{cases}$
직교(Orthogonal)
내적이 영인 두 벡터
벡터의 길이 또는 노름(norm)
$$\bf \lVert a \rVert = \sqrt{(a,a)} (\geq 0)$$
$n$차원 Euclid 공간
$$\bf (a,b) = a^Tb = a_1b_1 + \cdots + a_nb_n$$
위 식과 같이 약속된 내적이 정의되었다고 하면, 이 때 이 공간을
$n$차원 Euclid 공간이라 부르고 $E^n$(또는 $R^n$)이라 표기한다.
- Euclid 노름(Euclidean norm)
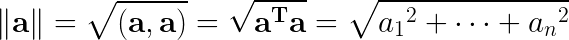
단위벡터(Unit Vector)
길이가 1인 벡터
Cauchy-Schwarz 부등식
$$\bf \lvert (a,b) \rVert \geq \lVert a \rVert \lVert b \rVert $$
삼각부등식
$$\bf \lVert a+b \rVert \geq \lVert a \rVert + \lVert b \rVert $$
평행사변형 등식
$$\bf {\lVert a+b \rVert}^2 + {\lVert a-b \rVert}^2 = 2({\lVert a \rVert}^2 + {\lVert b \rVert}^2) $$
일차변환(Linear Transformations)
- $\bf X$에서 $\bf Y$로의
사상(mapping)또는변환(transformation),연산자(operator)- 공간 $\bf X$의 벡터 $\bf x$에 대하여 공간 $\bf Y$의 유일한 벡터 $\bf y$를 대응(이와 같은 사상을 $\bf F$와 같은 대문자로 표기하자)
- 공간 $\bf X$의 벡터 $\bf x$에 대응하는 $\bf Y$의 벡터 $\bf y$를 $\bf F$에 의한 $\bf x$의
상(image)이라 하고 $\bf F(x)(또는 괄호 없는 Fx)$로 표시한다.
- $\bf F$를
선형사상(linear mapping)또는일차변환(linear transformation)- $\bf X$의 임의의 벡터 $\bf v, x$와 임의의 스칼라 $c$에 대하여 다음의 식을 만족
$$\bf F(v + x) = F(v) + F(x)$$
$${\bf F}(c {\bf x}) = c{\bf F}({\bf x}) $$
- $\bf X$의 임의의 벡터 $\bf v, x$와 임의의 스칼라 $c$에 대하여 다음의 식을 만족
$R^b$ 공간에서 $R^m$ 공간으로서의 선형변환
$\bf X = R^n$, $\bf Y = R^m$이라 하자 $m \times n$ 행렬 $\bf A$가 주어지면 $R^n$에서 $R^m$으로 의 변환
$$\bf y = Ax $$
$\bf A(u + x) = Au + Ax$와 ${bf A}(c{bf x}) = c\bf{ A x}$이므로 이 변환은 선형이다.
$\bf F$는, $\bf R^n$과 $\bf R^m$ 공간에 각각 주어진 기저를 이용하여, 적절한 $m \times n$행렬 $\bf A$로 나타낼 수 있다.
http://contents2.kocw.or.kr/KOCW/document/2016/hanbat/kimdongsoo/7.pdf
https://latexbase.com/d/e2c4eeb2-68f6-4efa-a305-112097ad9e8b
https://forknwork.wordpress.com/2018/02/14/openpose3d-pose-baseline/
https://github.com/wangzheallen/awesome-human-pose-estimation#3d-pose-estimation


