Robot Manipulator and Underwater Robot Application 6주차 6-2 Relative Velocities of Moving Frames(1)

Relative Velocities of Moving Frames

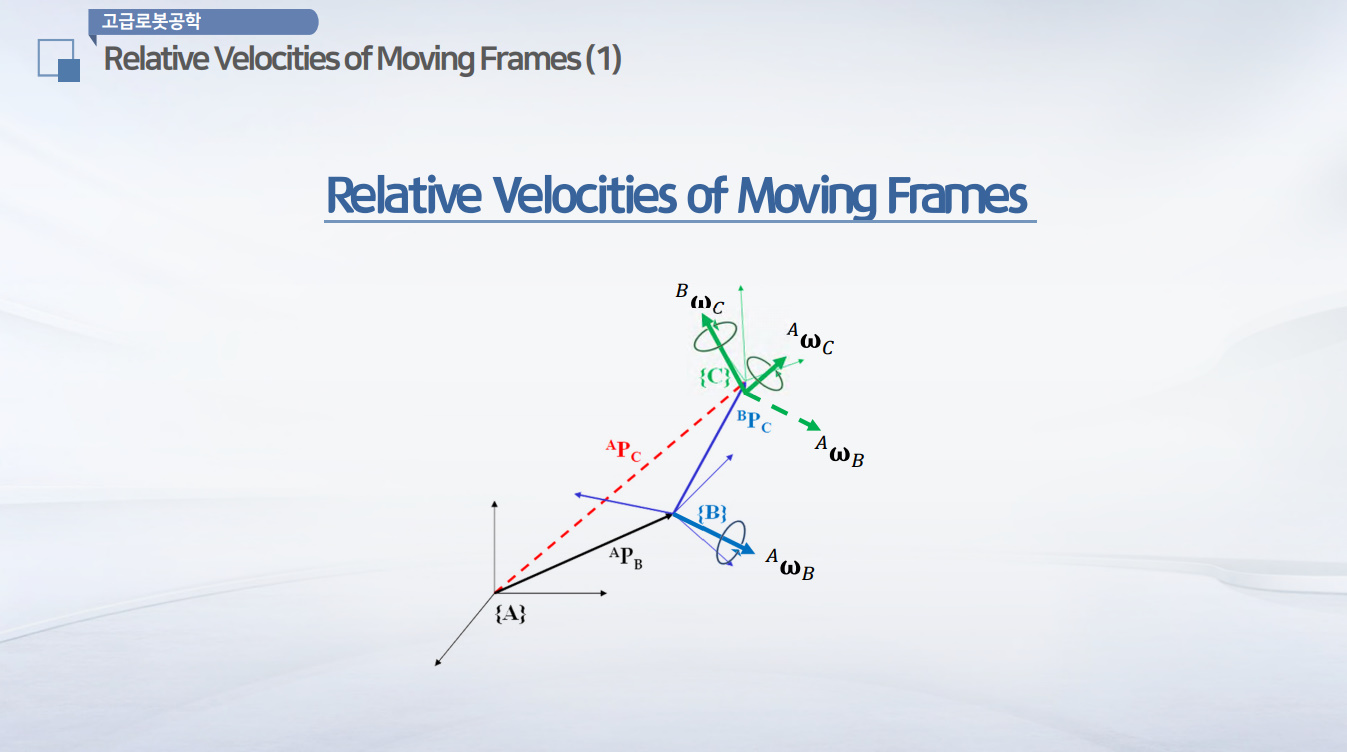
세 개의 프레임을 한번 생각해보면 위 그림처럼 A B C라고 하는 세개의 프레임이 존재하고 이랬을 때 A는 고정되어 있습니다.
A는 고정되어 있고 A에 대해서 B는 움직이고 B에 대해서 역시 C는 움직이고 있습니다. 자 이랬을 때 우리는 A라는 고정된 프레임에서 C라는 프레임의 원점의 좌표를 원점의 운동을 기술해보고 싶은 것입니다.

그렇다면 간단한 벡터관계식에 의해서 우리는 A프레임에 대한 C프레임의 원점을 $^AP_C$라고 이렇게 옆에 식처럼 표현할 수가 있고
이 좌표는 직접적으로 구하는 것이 아니라 간접적으로 B프레임까지 가서 다시 B프레임에서 C프레임까지 가는 그 과정으로 이 값들을 정의할 수 있겠습니다. 그랬을 때 B프레임 즉 A프레임에 대한 B프레임의 원점에 대한 좌표를 APB라고 하고 그 플러스 B프레임에 대해서 C프레임의 원점에 대한 좌표가 결국에는 BPC로 그렇게 정의가 됩니다.
이렇게 정의된 것을 그대로 쓰는 것이 아니라 A프레임으로 가지고 와야 됩니다. 그 A프레임으로 가지고 오는 매트릭스의 변화를 로테이션 매트릭스라고 합니다.
최종적으로는 C라는 프레임의 원점을 A프레임으로 가지고 오기 위해서는 B프레임을 A프레임으로 기술한 포지션과 C프레임을 A로 가지고 오기 위한 B프레임까지 갔다가 rotation되서 오는 벡터 두 개의 합으로써 표현할 수가 있을 것입니다.

이렇게 표현되어 있는 벡터, 위치관계식을 가지고 속도관계식을 얻으려고 하는 것인데 속도관계식을 얻기 위해서 미분을 양변에 해보도록 하겠습니다.
그랬을 경우에 앞에 C프레임의 원점을 A프레임으로 가져오는 포지션 벡터 P를 미분한 $\dot P$은 결과적으로는 B프레임으로부터 A프레임으로 오는 사이의 translation vector인 $\dot P$ + matrix 형태로 곱해져있는 rotation matrix와 P가 곱해져 있는 것을 미분한 형태로써 주어지게 되겠고 여기에서 A프레임은 고정되어 있기 때문에 B프레임까지 가는 그 속도관계식은 그대로 그냥 사용을 하면 되겠는데 moving frame일 경우에는 그 rotation하는 rate, 그 내용들 때문에 속도관계식이 조금 복잡해집니다. 그래서 일단은 그러한 관계식을 수식적으로 analytic 하게 계산을 해 보도록 하겠습니다.

그래서 여러분들 잘 아시는 것 처럼 두 개의 어떤 항이 있을 때의 미분은 앞에 것 미분 뒤에 것 미분 그런 방식으로 하는 것을 잘 알고 계실 것 입니다.
그래서 위에 보이는 식처럼 파랗게 표현한 부분은 일단은 로테이션 매트릭스를 미분한 것과, 그 다음에 뒤의 것은 그대로 놔둔 즉, C에서부터 B까지 오는 C프레임의 원점을 B로 가져오는 위치, 그 다음에 플러스 rotation matrix 에다가 B프레임에 대한 C프레임의 이동속도 $\dot P$, 이렇게 표현이 되겠습니다.
여기에서 각각의 Linear속도, 즉 translation 하는 속도는 큰 문제가 없습니다. 그대로 사용하면 되겠는데 여기에서 $d \above 1pt dt$ 그 다음에 R 로테이션 매트릭스에 대한 미분, 이 부분은 조금 다루기가 까다로울 수가 있습니다.
rotation matrix를 가지고 있습니다. 그럼 미분을 하면 그대로 사용을 하면 됩니다. 하지만 그랬을 때 이 로테이션 매트릭스에 대한 미분이 가지고 있는 정확한 물리적인 의미를 설명하는 것은 조금 어려울 수가 있겠습니다.
그래서 이러한 부분들을 잘 설명하기 위해서 이 rotation matrix를 미분하는 그 과정을 한번 차근차근 살펴보도록 하겠습니다.

그에 앞서서 로테이션 rate 을 보통 $\omega$라고 정의하는데 이 $\omega$는 사실 어떠한 프레임이 회전하는속도, 즉 각속도를 의미하는데 이 프레임이 회전하는 각속도라는 것이 사실상 그 프레임에서의 어떤 벡터로써 나타낼수 있습니다.

이제 이것을 더 이상 각속도라 생각하지 않고 이 로테이션 하는 이 벡터, 로테이션 벡터, $\omega$라고 하는 하나의 벡터, 로테이션이라고 하는 것은 잊어버리고 그냥 벡터다라고 가정을 한다면 이 벡터 자체로는 앞에서 위치관계식과 비슷하게 $\omega$는 A에서 표현되는 $\omega$ C프레임의 회전 각속도 $\omega$는 A프레임에서 표현되는 B프레임의 각속도에다가
로테이션 매트릭스를 포함하는 C프레임의 회전 각속도를 B프레임에서 기술한 이 방식, 즉 위치관계식과 그대로 일치하는 이런 수식을 보실 수 있겠습니다. 이렇게 표현이 되었고 그렇다면 앞서서 보여드렸던 rotation matrix를 미분하는 관계식 rotation matrix에 대한 미분이 물리적 의미, 수학적 의미를 가지는지를 살펴보도록 하겠습니다.

먼저 또다른 그래프를 가지고 왔는데요. 0번째 프레임이 위에서 보이는 그림에서 0번째 프레임은 고정된 프레임 입니다. 그리고 이 고정된 프레임에 대해서 첫번째 프레임, 1번 프레임이 존재한다고 가정을 하고 이 첫번째 프레임은 0번째 프레임에 대해서 $\omega$라는 velocity로, $\omega$라는 각속도를 가지고 회전을 하고 있습니다. 첫번째 프레임에 고정되어 있는 벡터 s라는 것이 존재한다 s라는 그러한 벡터가 있었을 경우에 회전하는 각속도 $\omega$와 벡터에 대한 미분과 이런것들이 어떻게 표현되는지 살펴보도록 하겠습니다.
옆에 그림에서 s가 $\omega$에 의해서 회전을 통해서 새로운 s로 바뀌게 됐을 때, 그 둘 사이에 $\Delta s$ 즉 s의 변량, 변화량을 어떻게 정의할 수 있냐면 위에 그림에서 만약에 이 $\omega$에 의해서 아주 빠르게 아주 작은 시간동안 돌았다라고 한다면
$\Delta s$는 결과적으로 위에 보이는 식에서 A에서부터 B까지의 그 변화량이 결국에는 $\Delta s$ 즉 s의 변화량이 되겠습니다.
그러면 위에 그림에서 $\overline{AB}$는 $\overline{AC}$라고 불리는 회전축, 회전축까지의 거리에다가 $\Delta \theta$, 이 끼인각인 $\Delta \theta$로 표현을 할 수가 있겠습니다.
이게 만약에 굉장히 긴 변이라면 이렇게 표현이 안되겠지만 짧은 변이 굉장히 짧은시간 동안에 회전이 이뤄지는 경우에는 이 미분관계식에 의해서 $\Delta \theta$ 즉 $\overline{AC} |\Delta \theta|$는 AB하고 같다라고 표현할 수 있습니다.
이렇게 표현했을 때 여기에서 이 $\overline{AC}$라고 하는 것은 다시 s전체, 고정되어 있는 벡터 s에다가 $sin \phi$를 곱해주면 결과적으로 이 $\omega$축 방향으로의 내려가는 그 길이만큼
즉 $\overline{AC}$만큼의 길이를 구할 수 있겠죠. 즉 $\overline{AC}$는 s의 절대값에다가 $sin \phi$ 즉 s의 크기에다가 $sin \phi$로써 $\overline{AC}$를 정의할 수가 있겠고요. 위에 그림에서의 $\angle AOC = \phi$라고 얘기합니다.
그리고 $\Delta \theta$라고 하는 것은 $\omega$의 속도로 현재 돌고 있다고 말씀드렸습니다.
그래서 $\omega$ 곱하기 $\Delta t$만큼 즉, $\Delta t$만큼 $\omega$의 속도로 돌면 그게 결국에는 $\Delta \theta$라고 표현이 됩니다.
따라서 결국 $\Delta s$는 $\overline{AB}$로 표현되고, $\overline{AB}$는 $\overline{AC}$의 $\Delta \theta$로 표현되고, 다시 이것들은 금방말씀드린 것 처럼 s의 크기와 $\omega$의 크기와 $sin \phi$의 $\Delta t$만큼으로 표현이 될 것 입니다.
이렇게 s하고 $\omega$하고 $sin \phi$하고 $\Delta t$로 표현이 되는데 이때 $\Delta t$를 양변에 나눠주게 되면 보이는 식처럼 $|\Delta s| \above 1pt \Delta t = |s||\omega| sin \phi$라고 표현이 됩니다.
즉, s하고 $\omega$ 라는 두 개의 벡터에 의한 cross product, 즉 $\omega X s$라고 하는 cross product의 절대량이라는 것을 알 수가 있습니다.
이렇게 $\omega X s$에 대한 크기로써 $\Delta s \above 1pt \Delta t$를 설명할 수가 있겠고요. 자 이랬을 때 그렇다면 이 $\omega$ 크로스 s가 나타내는 방향은 어디일까요.
$\omega X s$를 한번 여러분이 생각해보시면 $\omega$하고 s하고 이루는 각도에 대해서 $\omega X s$에 대해서 오른손법칙을 적용하게 되면
결과적으로는 $\overline{AB}$ 방향하고 수평되는 같은 방향을 나타낸다는 것을 알 수 있습니다. 자 그러면 어떤 벡터가 존재하고요 그 벡터의 크기는 $|\omega X s|$고
그 벡터의 방향은 $\omega X s$방향이다라고 한다면 이 벡터는 뭐가 될까요.
바로 그냥 $\omega X s$가 되겠죠. 즉, s를 시간에 대해서 미분한 것은 $\omega X s$로써 표현될 수 있기 때문에 옆에 보이는 식처럼 $\dot s$ 이라고 하는 것은 $\omega X s$로 표현이 되겠습니다.
그렇게 표현이 된 것을 이용해서 rotation matrix에 대한 미분을 한번 다른 방법으로 조금씩 조금씩 찾아보도록 하겠습니다.

일단은 rotation matrix가 존재할 때 이 rotation matrix는 앞서서 rotation matrix를 설명하는 방법이 세가지 정도 있다고 말씀을 드렸는데 그 중에서 한가지는 어떠한 A프레임에 대해서 B프레임에 X Y Z축에 대한 좌표계를 A프레임에 대해서 표현을 한 것으로 나타낼 수 있다라고 해서
옆에 보이는 수식처럼 로테이션 매트릭스는 각각 X벡터 Y벡터 Z벡터로 이뤄진 이러한 벡터로서 표현이 가능해 지고 C라는 점은 B프레임에서 기술되는 C라는 점은 X Y Z형태로 이렇게 표현을 풀어서 나눠서 써볼 수 있습니다.

그렇다면 지금 구하고 싶은 $d /above 1pt dt$ 로테이션 매트릭스의 그 C에서부터 B로 오는 포지션, translation 벡터, 이렇게 표현되는 것들을 옆의 식처럼 하나씩 풀어서 설명을 해 보겠습니다.
이 두 식을 rotation matrix를 각각 $d /above 1pt dt$ X, 그 다음에 $P_c$의 X 역시 마찬가지로 Y Z에 대해서도 똑같이 각각 로테이션 매트릭스를 벡터단위로 나누어 위에 식처럼 표현을 할 수 있습니다.
이건 계산상으로 수식적으로 풀어쓰면 똑같이 이렇게 나오게 되는 것이고요. 이 때 X Y Z라고 하는 각각의 좌표축들은 보시면 B라는 프레임에서의 A에 대한 각각의 좌표축입니다. 하나의 벡터들입니다.
조금 전에 회전하는 좌표프레임에 대해서 그 회전하는 각속도에 대해서 고정된 벡터에 대한 회전관계식을 어떻게 유도했나요?
바로 s가 주어졌을 때 그 $\dot s = \omega X s$로 주어진다고 말씀드렸습니다.
그래서 이 위에 식은 바로 아래처럼 $d /above 1pt dt$. 이 미분항들이 바로 $\omega X x$, $\omega X y$, $\omega X z$로써 이렇게 바꿔서 표현이 가능해 지고
분배법칙에 의해서 $\omega$를 전부다 묶으면 $XP_X YP_Y ZP_Z$ 이런식으로 옆에 식처럼 이렇게 묶어서 설명할 수 있겠고
이걸 다시 원래의 식으로 돌리면 원래의 로테이션 매트릭스 하고 그 다음에 포지션 벡터로서 표현을 한다면 마지막 식에서 보이는 것처럼 $\omega X R P$형태로서 이렇게 정리가 되겠습니다.
즉 $d/above 1pt dt (R) P$라고 하는 이러한 연산은 최종적으로는 $\omega X R P$ 의 형태로 주어지게 되는 것이죠.

여러분들이 앞에서 아까 제가 말씀드린 것처럼 직접적으로 $\omega$라고 하는 것은 rotation matrix에서 rotation matrix 사이에
정해진 축에 대해서 회전하는 그러한 방법으로 표현도 가능하다고 말씀드렸는데요. 그 회전하는 축과 관계식을 가지는지에 대한 설명이 되겠습니다.
일단 이러한 식을 전개하기 앞서 몇가지 트릭을 쓸텐데요. rotation matrix가 주어지고
그 rotation matrix는 이 자체로는 orthogonal한 형태를 띄게 됩니다.
그랬을 때 $R(t)$는 결과적으로 identity matrix가 되죠. 즉 transpose가 자기 자신의 역행렬이 된다는 것을 앞에서 여러 번 말씀드린적이 있습니다.
그래서 $R^T(t)$는 identity matrix가 된다는 것을 알 수가 있습니다.

이 식을 바탕으로 양 변을 그대로 미분해보겠습니다.
양변을 그대로 미분하면 identity matrix는 111로 구성되어있는 상수항이기 때문에, 즉 상수 매트릭스이기 때문에 미분하게 되면 0으로 사라지겠죠. 0 매트릭스가 만들어 질 것 입니다.
거기에다가 앞에 부분에서 $\dot R$ 미분한거 그 다음에 뒤에쪽 $\dot R , \dot R^T$을 미분한 것을 쓰게되면 이렇게 $\dot R(t) R^T(t) + R(t) \dot R^T(t) = 0$라고 하는 새로운 식이 만들어지게 되는 것입니다.
여기에서 조금 유념해서 보실 부분이 $\dot R R^T$ 하고 뒤에 $R \dot R^T$ 두 개의 식들은 가만히 보시면 트랜스포즈 관계식을 가지고 있다라는 것을 확인하실 수가 있겠습니다.
그렇다면 앞에 부분을 $S^T(t)$라고 정의를 해 보고요 $R(t) \dot R^T(t)$를 $S(t)$라고 정의를 하면, $S^T(t) + S(t) = 0$라고 하는 수식이 만들어지는 것입니다.

바로 이런 관계식을 가지고 있는 것을 skew-symmetric 매트릭스라고 얘기했었습니다. 즉 $S^T$가 자기자신에 -를 붙인것과 같다고 하는 것입니다.
그래서 트랜스포즈하고 자기자신을 더했을 때 0이 되는 그러한 매트릭스를 skew-symmetric 매트릭스라고 얘기 했습니다.
즉 S라고 하는 것은 $\dot R R^T$의 형태를 띄게 되고 이렇게 어떤 S가 아직 뭔지 모르겠지만 S를 $\dot R R^T$로 이렇게 만들어줄 수 있다라는 것입니다.
그랬을 때 $\dot R$은 다시 이 $S = \dot R R^T$ 에서 양변에다가 $R$을 곱해주게되면 결국에는 우측변에 있는 항에는 $\dot R$만 남게되겠고
좌측변에 있는 항이 $SR$의 형태로 주어지게 될 것 입니다.

이렇게 주어졌을 때 만약에 이 $\omega$라고 하는 두 좌표계상에서의 두 좌표계의 속도 관계식, 속도가 $\omega$로 회전을 하고 있다라고 했을 때
$\omega$는 $\omega$는 $\omega_x$ $\omega_y$ $\omega_z$ 라고 이렇게 표현을 할 수 있다고 말씀드렸는데 이 S하고 $\omega$하고 관계식이 분명히 있을 것 같다라는 추정으로 일단은 S를 $\omega$ S에 cross product 형태로 만들어보겠습니다.
과연 이 추정과 이런것들이 어떻게 뒤에서 연결되는지는 이어지는 설명에서 계속 말씀드릴텐데
이렇게 S를 표현하는데, 앞서서 cross product 를 설명할 때 S로 표현을 하기도 했었는데 이걸 조금 달리 $\omega X$ 라고 하는 이러한 rate으로 표현되는 이 형태로도 표현이 가능합니다.
그렇기 때문에 $a = Sb = [\omega X]b = \omega X b$이런 형태가 다 같은 것을 의미한다고 여러분들은 생각하면 되겠습니다.

이어서, 앞서 Rodrigues parameter, Rodrigues equation을 Euler’s theorem을 가지고 설명한 적이 있었는데 만약에 미소변이에 대해서 미소한 어떤 각도표현에 대해서 두 개의 로테이션 매트릭스는 곱하기 형태로 바꿔 쓸 수 있다.
즉 $t + \Delta t$에서 $\Delta t$가 굉장히 작은값이다라고 했을 경우에는 $R(\Delta t) R(t)$의 형태로 표현이 가능하다는 것을 말씀드린적이 있었고
이것을 Rodrigues equation을 가지고 설명을 쭉, 수식을 쭉 전개를 하면 옆에 보이는 식처럼
위 2번째 식의 형태로 표현이 되겠고
이 때 굉장히 작은 미소한 회전량을 설명하는 것이기 때문에 $sin(\Delta \delta)$를 결국에는 싸인값은 $\Delta \delta$로 바뀌게 되겠고
그다음에 $cos(\Delta \delta)$ 같은 경우에는 1의 값으로 바뀌어서 뒤의 항들이 사라지는 것을 앞에서 다룬 적이 있었습니다.
그래서 결과적으로는 $R (t + \Delta t)$는 밑에 보이는 식처럼 I의 identity matrix + $\Delta \delta$에 그 다음에 $[\lambda X]$에 $R(t)$의 형태로 이러한 수식으로 전개가 되겠습니다.
이때 $\Delta \delta$ 같은 경우에는 굉장히 작은 어떠한 미세한 미소 회전량이 되겠죠. 이런 미소 회전량에 대한 설명이 되겠습니다.

이렇게 주어졌을 때 로테이션 매트릭스를 정의를 할 때 로테이션 매트릭스에 dot, 즉 시간에 대한 미분은 수식적으로 어떻게 설명이 가능하냐하면
$R(t+\Delta t) - R(t) \above 1pt \Delta t$. 일반적인 함수에 대한 미분관계식과 똑같이 이렇게 표현한다면, 앞서서 $R(t + \Delta t)$라고 정의된 그 내용을 바로 대입을 해 보겠습니다.
그러면 아이덴티티 매트릭스가 있으니까 R에 대해서 소거가 되고 결과적으로 옆에 보이시는 것 처럼 limit, t를 $\Delta t$를 0으로 보낼 때 $\Delta \delta[\lambda X] R(t) \above 1pt \Delta t$고,
이랬을 때 여기에서의 유일한 작은 스몰 변량에 대한 미분관계식을 만드는 것은 바로 $\Delta \delta[\lambda X] R(t) \above 1pt \Delta t$ 그래서 이것들은 그렇게 미분해주게 되면 $\dot \delta [\lambda X]R(t)$ 람다하고 R같은 경우에는 각각 현재의 상수형태를 표현하고 있기 때문에 이렇게 $\dot \delta [\lambda X]R(t)$ 의 형태가 되겠고요
이 때 $\lambda$라고 하는 것은 로드리게스 파라미터에서 회전의 중심이 되는 축이되겠습니다. 회전의 중심이 되는 축이 되겠고요. 그 축에 대해서 $\dot \delta$만큼 즉 그 축에 대한 회전량이 되겠죠.
회전량만큼은 결과적으로 이게 어떤 축이 회전하는 그 양, 즉 $\omega$ 형태로 표현이 가능해지는 것이죠.
그래서 결국 이 식들은 옆에 보이는 식처럼 $\omega X$ 매트릭스 형태에다가 $R(t)$ 형태로 바꿔쓸수가 있게 되는 것이고
이것은 앞서서 직전에 $\omega X$를 S로 전개한 것과 마찬가지로 $SR$의 형태로 성립할 수가 있다는 것을 말씀드릴 수 있겠습니다.
최종적으로 $\dot R$이라고 하는 것을 어떻게 회전에 대한 식으로써 표현하는지에 대한 것들을 이제까지 쭉 정리를 해보았습니다.

[[cos{\theta_1},0,-sin{\theta_1},-sin{\theta_1}d_3],[sin{\theta_1},0,cos{\theta_1},cos{\theta_1}d_3]]
$
\left\lceil
\matrix{[cos{\theta_1} & 0 & -sin{\theta_1} & -sin{\theta_1}d_3 \cr sin{\theta_1} & 0 & cos{\theta_1} &cos{\theta_1}d_3 \cr 0 & -1 & 0 & d_1+d_2 \cr 0 & 0 & 0 & 1}
\right\rceil

$^0A_1 = Rot(Z_{0},\theta_1)Trans(Z_{0},d_1)Trans(X_1,a_1)Rot(X_1,\alpha_1) =$

$^1A_2 = Rot(Z_{1},\theta_2)Trans(Z_{1},d_2)Trans(X_2,a_2)Rot(X_2,\alpha_2) =$

$^2A_3 = Rot(Z_{2},\theta_3)Trans(Z_{2},d_3)Trans(X_3,a_3)Rot(X_3,\alpha_3) =$